Содержание статьи
Roadmap
Это пятый урок из цикла «Погружение в крипту». Все уроки цикла в хронологическом порядке:
- Урок 1. Исторические шифры. Основы и исторические шифраторы. Как работают (и анализируются) шифры сдвига, замены, Рихарда Зорге, шифр Вернама и шифровальные машины
- Урок 2. Распределение ключей. Что это такое, как выполняется распределение ключей и как выбрать криптостойкий ключ
- Урок 3. Современные отечественные шифры. Что такое сеть Фейстеля и какими бывают отечественные блочные шифры, используемые в современных протоколах, — ГОСТ 28147—89, «Кузнечик»
- Урок 4. Современные зарубежные шифры. В чем разница между 3DES, AES, Blowfish, IDEA, Threefish от Брюса Шнайера и как они работают
- Урок 5. Электронная подпись. Виды электронных подписей, как они работают и как их использовать (ты здесь)
- Урок 6. Квантовая криптография. Что это такое, где используется и как помогает в распределении секретных ключей, генерации случайных чисел и электронной подписи
Как работает цифровая подпись
Если вспомнить формальное определение, то ЭЦП — это реквизит электронного документа. Другими словами, последовательность битов, вычисленная уникально для каждого конкретного сообщения. Подпись может быть вычислена как с применением секретного ключа, так и без него. Без секретного ключа подпись представляет собой просто код, который может доказать, что документ не был изменен. С использованием секретного ключа подпись докажет целостность сообщения, позволит убедиться в его подлинности и аутентифицировать источник.
Если ты читал вторую часть нашего цикла, то помнишь, что существуют симметричный и асимметричный подходы к шифрованию. С электронной подписью дела обстоят очень похоже — есть подписи с симметричным механизмом, а есть с асимметричным.
Симметричный механизм подписи малоприменим на практике — никому не хочется генерировать ключи для каждой подписи заново. А как ты помнишь, именно в одинаковых ключах кроется фишка симметричной криптографии.
- В лучших традициях асимметричной криптографии — имеем пару открытый и секретный ключ. Но не спеши пролистывать все это описание. Электронная подпись концептуально отличается от шифрования применением ключей, описанного ранее.
- От документа или сообщения подсчитывается хеш-функция, которая сократит сообщение любого объема до определенного количества байтов.
- Посредством криптографических преобразований вычисляется сама электронная подпись. В отличие от асимметричного шифрования, подпись основана на закрытом ключе, а вот проверить с помощью открытого ключа ее может любой его обладатель. Если помнишь, в шифровании все происходит наоборот: шифруют для нас на открытом ключе, а вот расшифровывать мы будем с помощью секретного ключа.
- Электронная подпись предоставляется вместе с исходным документом на проверку. По полученной композиции можно доказать, что документ с момента вычисления подписи не был изменен.
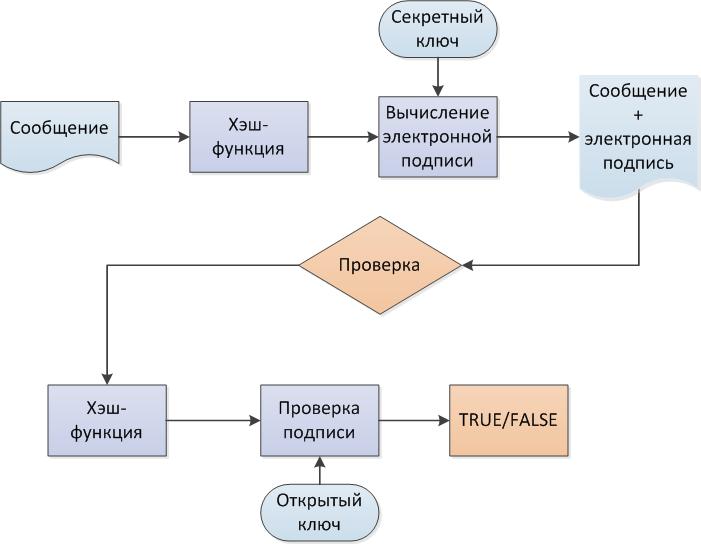
Схемы электронной подписи так же многообразны, как и способы шифрования. Чтобы схема подписи была стойкой, нужно, чтобы она основывалась на трудновычислимой математической задаче. Есть два типа таких задач: факторизация больших чисел и дискретное логарифмирование.
Факторизация больших чисел
Рассмотрим на практике электронную подпись на основе знаменитого алгоритма RSA. Шифрование RSA мы рассматривать не стали — это мейнстрим, и в той же «Википедии» есть его подробное описание.
1. Генерация ключей
Причина стойкости RSA кроется в сложности факторизации больших чисел. Другими словами, перебором очень трудно подобрать такие простые числа, которые в произведении дают модуль n. Ключи генерируются одинаково для подписи и для шифрования.
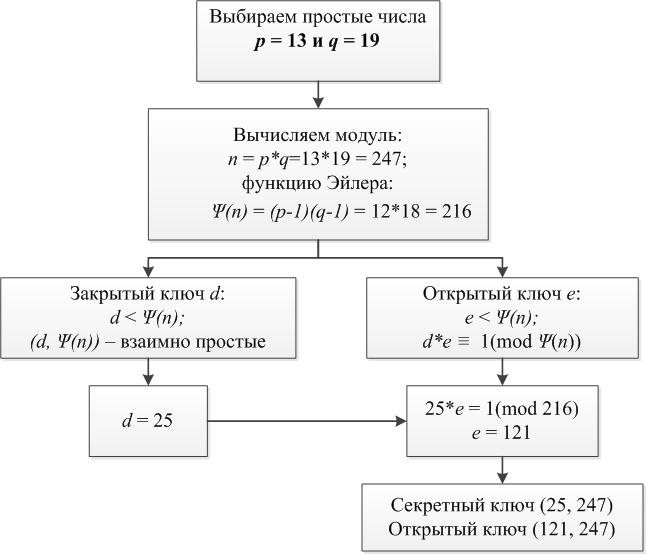
Когда ключи сгенерированы, можно приступить к вычислению электронной подписи.
2. Вычисление электронной подписи
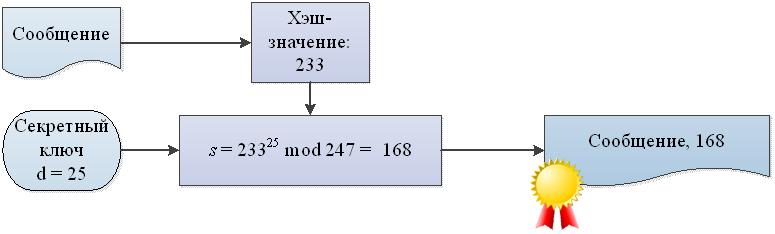
3. Проверка электронной подписи
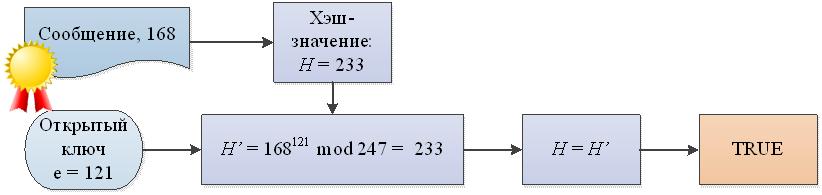
RSA, как известно, собирается уходить на пенсию, потому что вычислительные мощности растут не по дням, а по часам. Недалек тот день, когда 1024-битный ключ RSA можно будет подобрать за считаные минуты. Впрочем, о квантовых компьютерах мы поговорим в следующий раз.
В общем, не стоит полагаться на стойкость этой схемы подписи RSA, особенно с такими «криптостойкими» ключами, как в нашем примере.
Дискретное логарифмирование
Это вторая сложная проблема, на которой основаны цифровые подписи. Для начала хорошо бы усвоить, что такое дискретный логарифм. Для кого-то такое словосочетание может звучать пугающе, но на самом деле это одна из самых простых для понимания вещей в этой статье.
Предположим, дано уравнение 4x = 13 (mod 15). Задача нахождения x и есть задача дискретного логарифмирования. Почему же она так сложна для вычисления? Попробуй решить это уравнение перебором! Компьютер, ясное дело, будет более успешен, но и задачи дискретного логарифмирования обычно далеко не так просты. Возьмем для примера схему Эль-Гамаля.
1. Генерация подписи

2. Проверка подписи
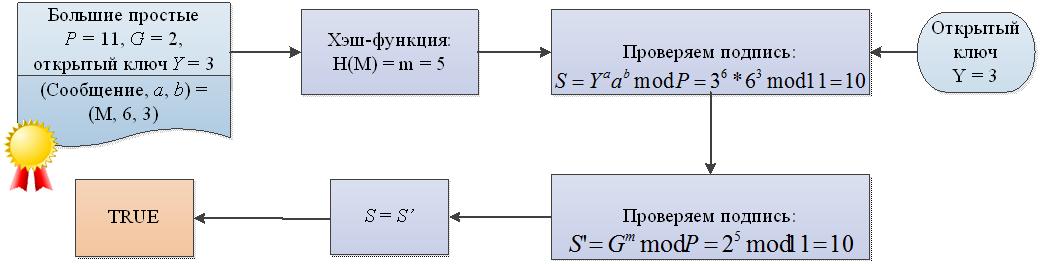
Даже если не вникать в схему, понятно, что такой алгоритм сложнее. Кроме того, нигде уже не используется простой модуль, его сменили эллиптические кривые. Эллиптическая кривая — это кривая, которая задана кубическим уравнением и имеет невообразимо сложное представление. Задача решения логарифма в группе точек, которые принадлежат эллиптической кривой, вычислительно сложная, и на данный момент не существует таких мощностей, которые решали бы это уравнение за полиномиальное время, если длина секретного ключа составляет 512 бит. Согласно задаче дискретного логарифмирования, невероятно сложно найти на кривой две такие точки, которые связывает операция возведения в некоторую степень.
ЭЦП на практике
В России, как и во многих развитых странах, электронная подпись имеет официальный юридический статус. У нас этот факт регламентирует закон № 63-ФЗ «Об электронной подписи». Однако он утверждает, что юридической силой обладает далеко не любая электронная подпись, а только соответствующая определенным критериям:
- подпись сгенерирована посредством криптографического преобразования с секретным ключом;
- этот ключ и соответствующий ему открытый ключ выданы квалифицированным удостоверяющим центром;
- по подписи можно достоверно установить ее обладателя.
Подпись также должна быть вычислена средствами, соответствующими требованиям закона. Этим требованиям удовлетворяет отечественный алгоритм шифрования ГОСТ 34.10—2012. Он использует математический аппарат эллиптических кривых, является достаточно стойким и официально используется для разработки криптографических средств, реализующих электронную подпись. Для того чтобы попробовать неквалифицированную подпись — без сертификата удостоверяющего центра, можно воспользоваться известной PGP. Потестировать подпись можно, к примеру, на сайте ReadVerify.
Стоит сказать, что в нашей стране электронная подпись используется чаще, чем можно себе представить. В банках, налоговых, торгово-закупочных операциях, бухгалтерии — во всех этих организациях используется или внедряется ЭЦП. Электронная подпись отважно борется со злом бюрократии, однако до полной победы еще далеко.
За рубежом электронный документооборот процветает еще дольше. Официальный стандарт электронной подписи в США DSS (Digital Signature Standard) также использует эллиптические кривые и основан на описанной выше схеме Эль-Гамаля.
Цифровая подпись в Bitcoin
Помимо прочего, электронная подпись используется в криптовалютах, в частности — в Bitcoin. У каждого пользователя Bitcoin есть пара из секретного и открытого ключа. Хеш-значение открытого ключа служит основным адресом для передачи монет. Это значение не секретно, и сообщать его можно кому угодно. Но по значению хеша вычислить значение открытого ключа невозможно.
Сама пара ключей будет использована лишь однажды — при передаче прав собственности. На этом жизнь пары ключей заканчивается.
- PUB1 — публичный ключ;
- PRIV1 — секретный ключ;
- HASH1 или HASH(PUB1) — хеш-значение открытого ключа (биткойн-адрес);
- HASH2 или HASH(PUB2) — хеш открытого ключа следующего владельца.
Вот как устроен сам процесс передачи прав собственности на биткойны.
- Владелец монеты открыто сообщает хеш своего публичного ключа HASH(PUB1), это и будет идентифицировать биткойн.
- До момента продажи оба ключа PUB1, PRIV1 продавца остаются в секрете. Известен только HASH(PUB1) и соответствующий ему биткойн.
- Как только появляется покупатель, владелец формирует открытое письмо, в котором указывает адрес биткойна HASH(PUB1) и хеш-значение публичного ключа нового владельца HASH(PUB2). И конечно же, подписывает письмо своим секретным ключом PRIV1, прилагая публичный ключ PUB1.
- После этого пара ключей владельца PUB1 и PRIV1 теряют свою актуальность. Публичным ключом можно проверить само письмо, узнать новый адрес монеты.
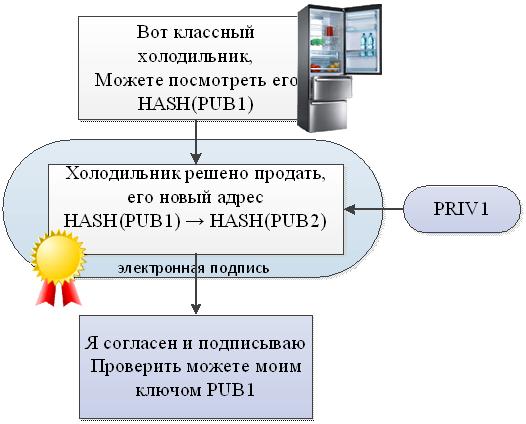
О втором собственнике ничего не известно, кроме HASH(PUB2), до тех пор пока он не передаст права третьему владельцу. И эта цепочка может быть бесконечной.
Подписывая передачу прав с использованием ЭЦП, собственник подтверждает не только свою личность, но и свое согласие на проведение сделки. То есть вернуть монетку он уже не может и с этим согласился, подписавшись электронной подписью.
Благодаря HASH(PUB) получается двойная защита. Первая загадка — узнать публичный ключ по его хешу. Вторая загадка — подписаться чужим секретным ключом.
Такая технология построения цепи передачи прав и называется блокчейном. Благодаря этой технологии можно отследить историю владения до самых истоков, но изменить эту историю никак нельзя.
Выводы
Будущее неразрывно связано с криптографией. В один прекрасный момент при получении паспорта наши дети будут генерировать электронную подпись и покупать чипсы в ларьке за криптовалюту. Что готовит нам будущее с точки зрения развития криптографии, посмотрим в следующей статье на примере квантовых компьютеров.