Криптография под прицелом. Атаки по второстепенным каналам для «уверенных»

Шаг 0. Данные и формат

Для этой статьи были исполь­зованы дан­ные с самых пер­вых сорев­нований DPA contest, которые теоре­тичес­ки до сих пор мож­но ска­чать с сай­та. К сожале­нию, дос­туп к этим дан­ным есть не всег­да, поэто­му я сох­ранил дан­ные для одно­го клю­ча и раз­местил их у себя на Ян­декс.Дис­ке.

Би­нар­ный файл, который дос­тупен на Яндекс.Дис­ке, называ­ется DES_DPA_1.hws. Он сос­тоит из заголов­ка и дан­ных. В заголов­ке ука­зана сле­дующая информа­ция (весь заголо­вок занима­ет 21 байт):

1. Пер­вые пять байт — магичес­кое сло­во HWSec, которое я исполь­зую для инди­кации фай­лов с дан­ными.
2. Сле­дующие четыре бай­та типа unsigned int пред­став­ляют собой количес­тво шиф­рований. В рас­смат­рива­емом слу­чае было выпол­нено 2000 шиф­рований и для каж­дого были записа­ны исходный текст, шиф­ротекст и изме­рена кри­вая нап­ряжения — все эти зна­чения пред­став­лены в бло­ке дан­ных.
3. Сле­дующие четыре бай­та типа unsigned int пред­став­ляют собой количес­тво точек в каж­дой кри­вой нап­ряжения. В рас­смат­рива­емом слу­чае это чис­ло рав­но 20 003.
4. За­тем сле­дуют восемь байт клю­ча алго­рит­ма DES. Все шиф­рования в ука­зан­ном фай­ле были сде­ланы с клю­чом 0x656A78656A7865.

За заголов­ком сле­дуют бло­ки дан­ных для каж­дого шиф­рования, сос­тоящие из исходно­го тек­ста, шиф­ротек­ста и кри­вой нап­ряжения. Количес­тво бло­ков для дан­ного фай­ла, ука­зан­ное в заголов­ке, рав­няет­ся 2000. Фор­мат этих дан­ных пред­став­лен в сле­дующем виде:

1. Во­семь байт исходно­го тек­ста.
2. Во­семь байт шиф­ротек­ста.
3. Са­ма кри­вая нап­ряжения, пред­став­ленная в виде мас­сива точек типа float. Количес­тво точек, ука­зан­ное в заголов­ке, рав­но 20 003.

Та­ким обра­зом, 2000 кри­вых нап­ряжения, в каж­дой из которой 20 003 точ­ки в фор­мате float, занима­ют 152 Мб. В более слож­ных сис­темах при­ходит­ся сни­мать нес­коль­ко мил­лионов кри­вых, поэто­му ты можешь пред­ста­вить объ­ем получа­емых дан­ных.

Шаг 1. Извлекаем данные

На пер­вом шаге давай прос­то попыта­емся извлечь дан­ные и пос­тро­ить одну кри­вую нап­ряжения. Я пред­лагаю это сде­лать на Python — он более гиб­кий, хотя обыч­но на вор­кшо­пах я даю код на С++, пос­коль­ку он быс­трее. Ты можешь так­же вос­поль­зовать­ся любым дру­гим язы­ком или сис­темой Matlab (Octave), R, Cobol или Brainfuck 🙂 на свое усмотре­ние.

Нам пот­ребу­ются допол­нитель­ные биб­лиоте­ки numpy, matplotlib и scipy, которые необ­ходимо уста­новить отдель­но (думаю, ты спра­вишь­ся сам без инс­трук­ций по уста­нов­ке биб­лиотек). Они нуж­ны для соз­дания гра­фиков и рас­чета дан­ных.

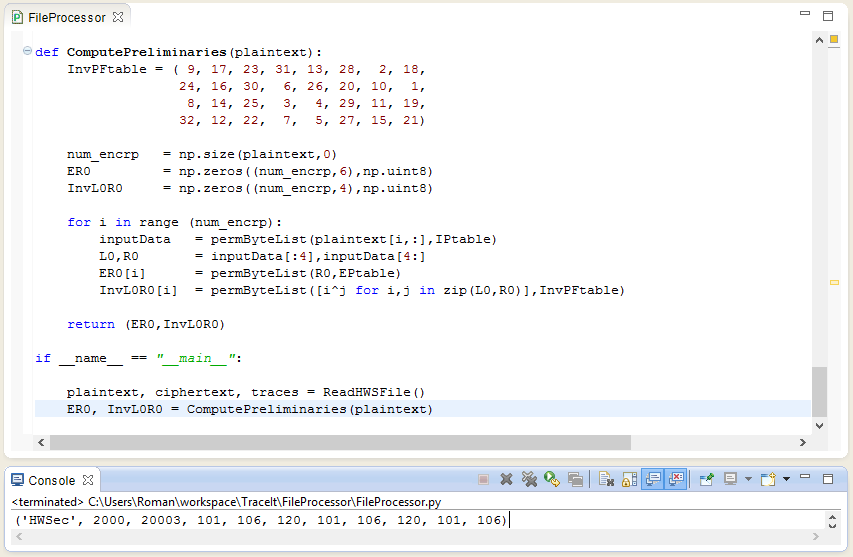
Сам код (и резуль­тат счи­тыва­ния заголов­ка фай­ла) при­веден на рис. 1. Файл DES_DPA_1.hws был сох­ранен в дирек­тории ../data, поэто­му в слу­чае дру­гого рас­положе­ния фай­ла изме­ни путь к нему. Как вид­но из стро­ки в кон­соли, заголо­вок был счи­тан кор­рек­тно.

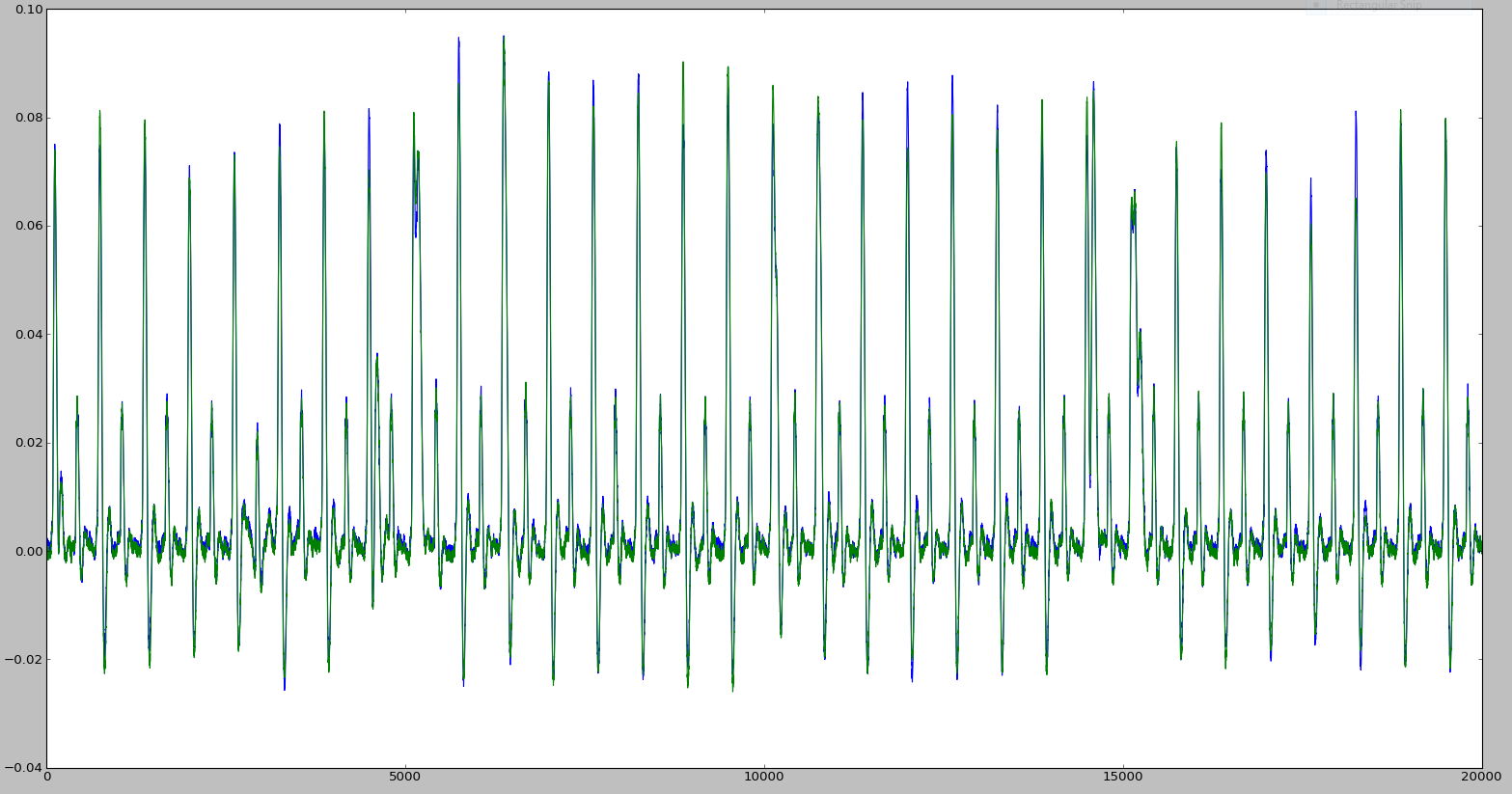
Ос­талось про­верить, были ли пра­виль­но счи­таны кри­вые нап­ряжения, — это опре­деля­ется прос­тым пос­тро­ением кри­вых для пер­вого и пос­ледне­го шиф­рований. На рис. 2 зеленым цве­том показа­на кри­вая для пер­вого шиф­рования и синим цве­том — для пос­ледне­го шиф­рования. Так как две кри­вые очень похожи, то дан­ные счи­таны кор­рек­тно, в про­тив­ном слу­чае воз­можны сдви­ги по оси Х или дру­гие изме­нения в гра­фиках.

На рис. 2 каж­дый боль­шой всплеск нап­ряжения про­исхо­дит в момент вос­ходяще­го сиг­нала осцилля­тора. Малень­кие всплес­ки меж­ду боль­шими про­исхо­дят в момент нис­ходяще­го сиг­нала осцилля­тора. В зависи­мос­ти от того, как спро­екти­рова­на сис­тема, регис­тры могут перек­лючать­ся как при вос­ходящем, так и при нис­ходящем сиг­нале с осцилля­тора. Я нас­читал 8 + 16 + 8 всплес­ков: пер­вые 8 так­тов исполь­зуют­ся для побай­товой переда­чи исходно­го тек­ста в крип­тогра­фичес­кий аксе­лера­тор, 16 так­тов исполь­зуют­ся для вычис­ления DES (один такт — один раунд), в оставши­еся 8 так­тов шиф­ротекст побай­тово переда­ется на выход. Эту информа­цию мож­но было про­читать в усло­виях кон­курса, но так­же ее мож­но про­верить с помощью методов вто­рос­тепен­ных каналов, как это показа­но на сле­дующем шаге.

Шаг 2. Проверка данных

Что­бы про­верить связь меж­ду переда­ваемы­ми дан­ными и пот­реблен­ной энер­гией, мы объ­еди­ним два метода, опи­сан­ные в пер­вых стать­ях. Во вто­рой статье говори­лось, что перек­лючение бита пот­ребля­ет энер­гию. Чем боль­ше битов перек­лючено, тем боль­ше энер­гии пот­ребля­ется. В пер­вой статье был опи­сан коэф­фици­ент кор­реляции Пир­сона, который поз­воля­ет срав­нить модель и реаль­ные дан­ные. Груп­пируя все вмес­те, мы получим инс­тру­мен­тарий для про­вер­ки нашей модели:

1. На пер­вом шаге пос­чита­ем количес­тво битов в пос­леднем бай­те исходно­го тек­ста. Получит­ся век­тор из 2000 эле­мен­тов (так как у нас 2000 исходных тек­стов).
2. За­тем возь­мем точ­ку i (для пер­вого раза i = 1) из каж­дой кри­вой нап­ряжения — получит­ся век­тор из 2000 эле­мен­тов (мы берем толь­ко одну точ­ку из каж­дой кри­вой нап­ряжения).
3. Пос­чита­ем коэф­фици­ент кор­реляции Пир­сона меж­ду моделью и век­тором нап­ряжения и сох­раним его.
4. Пе­рей­дем к сле­дующей точ­ке i и вер­немся на шаг 2.

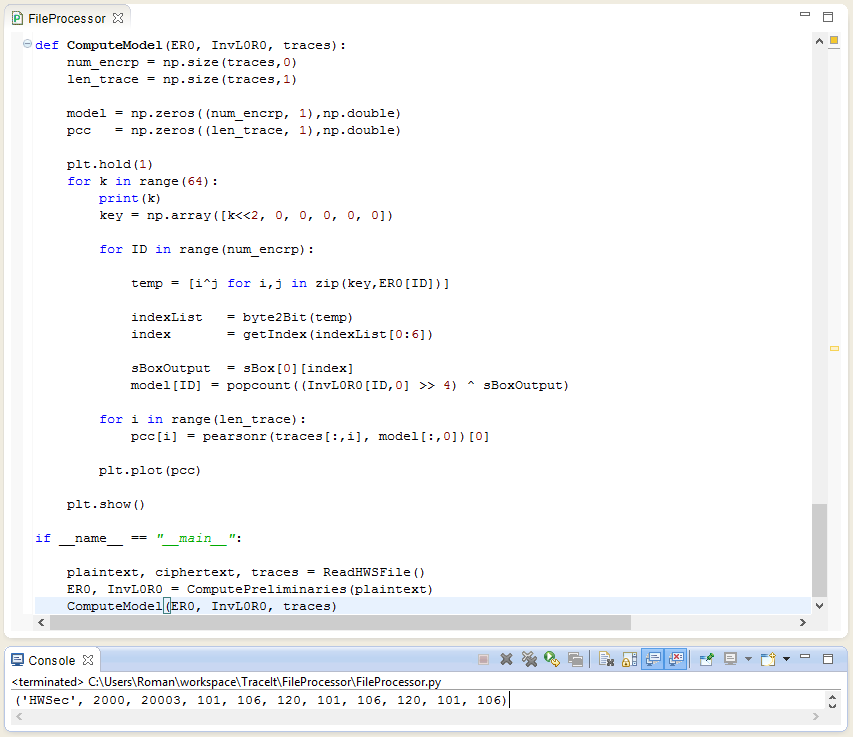
Ша­ги 2–4 будут выпол­нены 20 003 раза, то есть для всех момен­тов вре­мени, ког­да про­исхо­дило сня­тие нап­ряжения. Код это­го алго­рит­ма при­веден на рис. 3. Часть кода взя­та из Сети: фун­кция popcount воз­вра­щает количес­тво битов каж­дого эле­мен­та век­тора, переда­ваемо­го в качес­тве аргу­мен­та; а фун­кция CheckDataTransmission стро­ит кор­реляцию нашей модели и реаль­ных зна­чений нап­ряжения.

На рис. 4 при­веден гра­фик для ука­зан­ного кода, где крас­ным цве­том показа­но зна­чение кор­реляции, а синим цве­том — одна кри­вая нап­ряжения. Для срав­нения на рис. 5 показа­ны точ­но такие же гра­фики, но уже для 7-го бай­та исходно­го тек­ста, а на рис. 6 — для 6-го бай­та. На этих гра­фиках мы видим некото­рые всплес­ки, обус­ловле­ны они тем, что наша модель хорошо сог­ласу­ется с реаль­ными зна­чени­ями нап­ряжения. Мы так­же видим, что пик кор­реляции сме­щает­ся на один такт для каж­дого пос­леду­юще­го бай­та исходно­го тек­ста, — это лиш­ний раз показы­вает, что дан­ные переда­ются побай­тово. Ты можешь пос­тро­ить точ­но такие же гра­фики для бай­тов шиф­ротек­ста и пос­мотреть, что с ними слу­чит­ся.

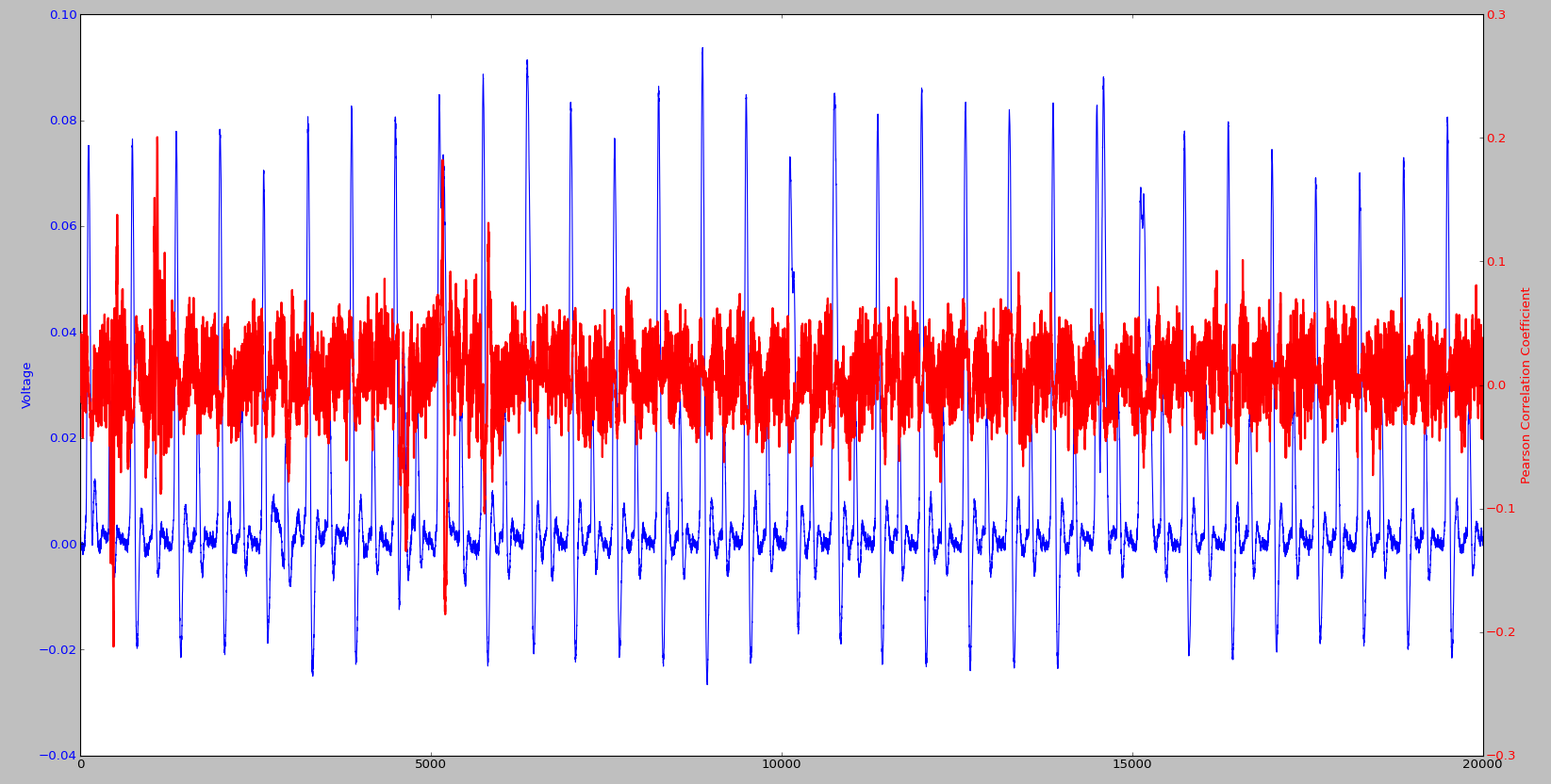
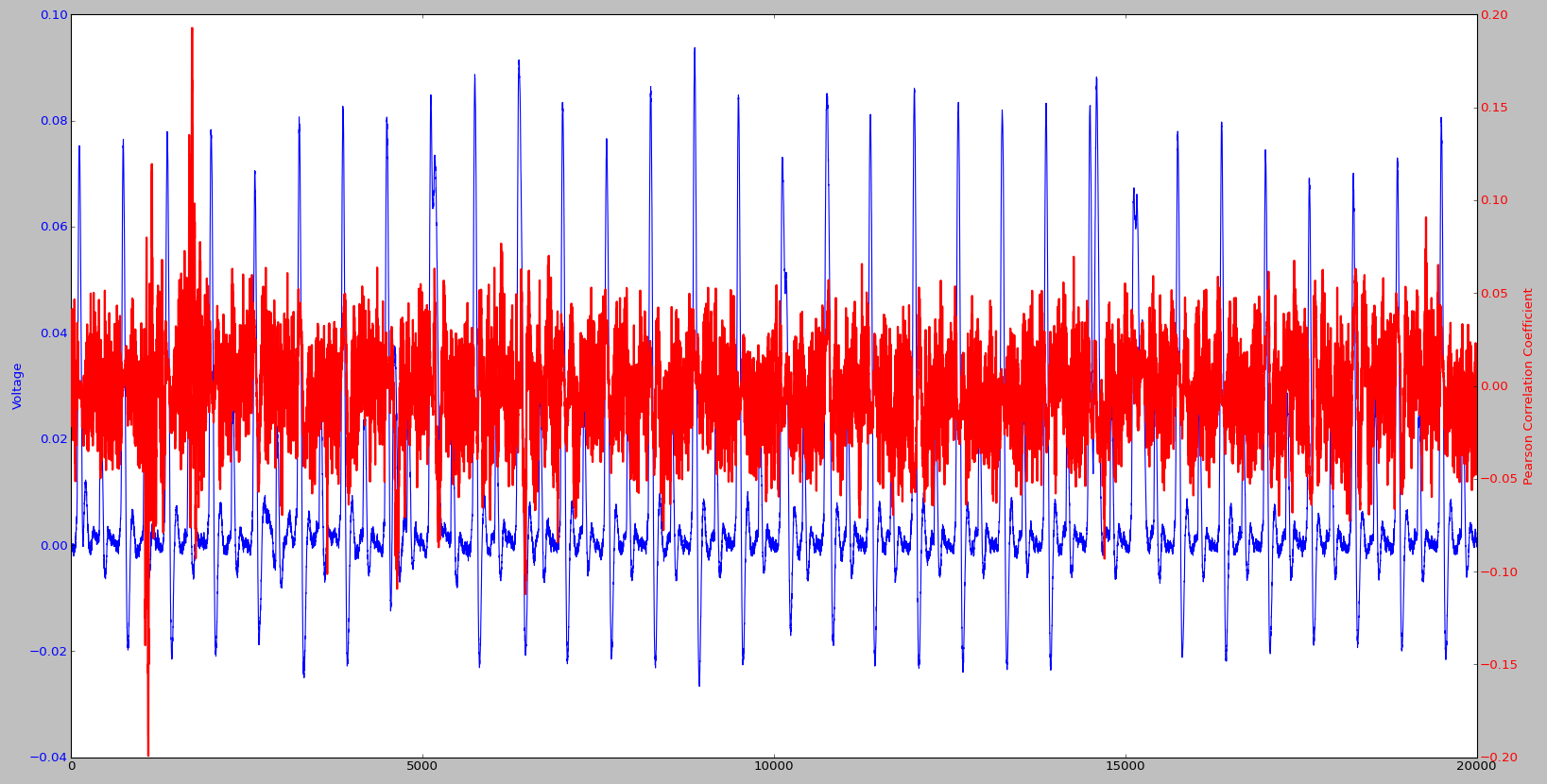
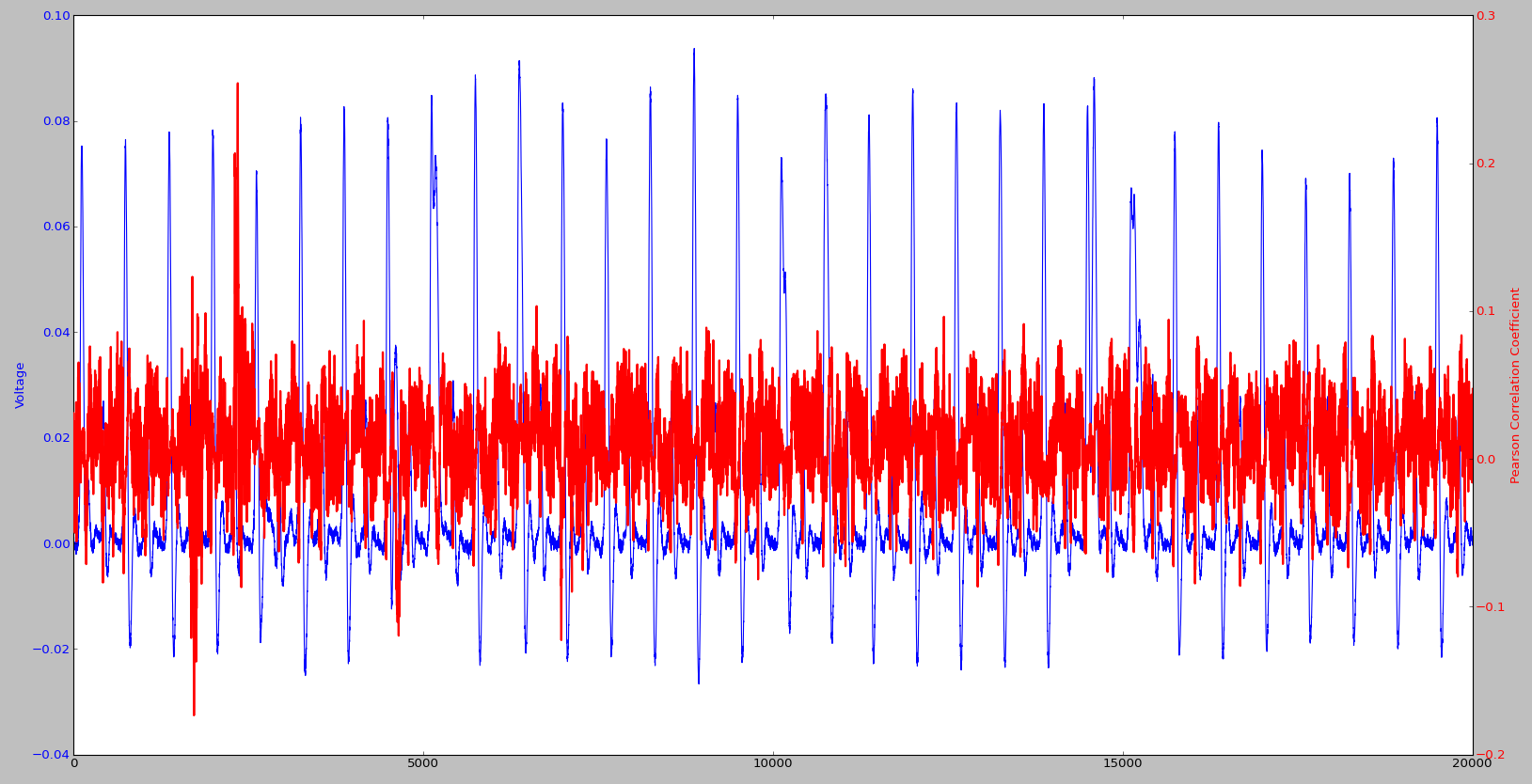
Шаг про­вер­ки дан­ных важен по двум при­чинам. Во‑пер­вых, за доволь­но корот­кое вре­мя мы смог­ли убе­дить­ся, что в дан­ной реали­зации есть связь меж­ду бинар­ными дан­ными и пот­реблен­ной энер­гией. Во‑вто­рых, мы смог­ли пос­мотреть, ког­да переда­ются дан­ные, то есть при­мер­но опре­делить момент начала работы алго­рит­ма (а он не может начать­ся рань­ше, чем получен весь исходный текст). Опре­деле­ние вре­мени работы алго­рит­ма поз­воля­ет сок­ратить окно иссле­дуемых кри­вых нап­ряжения, и это уско­ряет вре­мя обра­бот­ки.

Шаг 3. Разбираемся с реализацией алгоритма

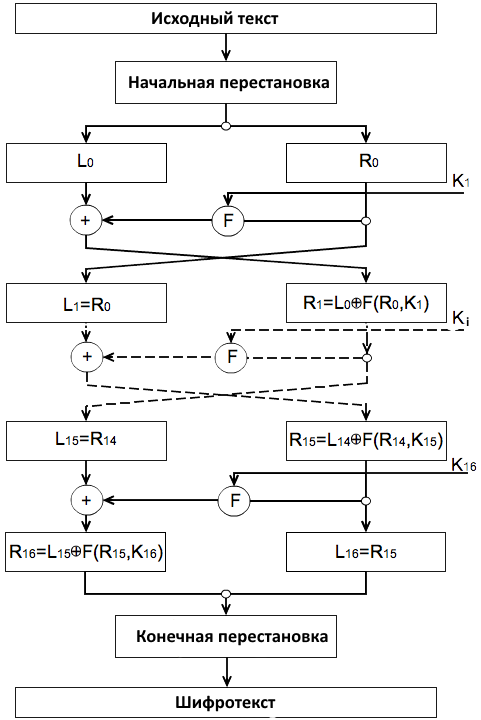
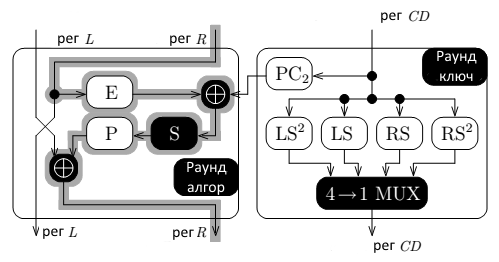
Ал­горитм DES, при­веден­ный на рис. 7, дол­жен быть тебе уже известен (если это не так, то поищи стан­дарт в Сети). Аппа­рат­ная реали­зация алго­рит­ма DES, которую мы ата­куем, при­веде­на на рис. 8. Эта схе­ма тре­бует пояс­нения. Вна­чале опи­шем бло­ки:

1. рег L — 32-бит­ный регистр, который сох­раня­ет левую часть сос­тояния алго­рит­ма пос­ле каж­дого раун­да.
2. рег R — 32-бит­ный регистр, который сох­раня­ет пра­вую часть сос­тояния алго­рит­ма пос­ле каж­дого раун­да.
3. рег CD — 48-бит­ный регистр, который сох­раня­ет раун­довый ключ.
4. E, P, PC2 — таб­лицы перес­танов­ки битов, а на деле прос­то соеди­нения.
5. S — таб­лица замеще­ния, выпол­ненная пол­ностью на логичес­ких бло­ках без памяти (в про­тив­ном слу­чае дол­жен быть регистр, который бы хра­нил зна­чения).
6. LS2, LS, RS, RS2 — опе­рации сдви­га, которые логич­но выпол­нять в виде соеди­нений.

Та­ким обра­зом, мы видим, что на каж­дом раун­де у нас про­исхо­дит вычис­ление зна­чений Li и Ri, которые переза­писы­вают пре­дыду­щие зна­чения Li-1 и Ri-1. Помимо это­го, раун­довый ключ тоже вычис­ляет­ся заново и переза­писы­вает пре­дыду­щее зна­чение регис­тра. Все эти переза­писи мож­но исполь­зовать для улуч­шения ата­ки, но мы сос­редото­чим­ся лишь на одном регис­тре L, так как его про­ще все­го модели­ровать.

Шаг 4. Разбираемся с моделью

Как и рань­ше, искать раун­довый ключ алго­рит­ма DES мы будем час­тями по шесть бит. Мень­ше не получит­ся, так как мы не смо­жем пос­тро­ить дос­товер­ные модели из‑за таб­лицы замеще­ния Sbox, которая заменя­ет шесть вход­ных бит четырь­мя выход­ными. Так как это незащи­щен­ная реали­зация алго­рит­ма DES, то зна­чения Li и Ri переза­писы­вают пре­дыду­щие зна­чения регис­тров. Таким обра­зом, зна­чение L1 переза­пишет­ся зна­чени­ем L2 на вто­ром так­те работы алго­рит­ма. Эта переза­пись вызовет всплеск нап­ряжения, который дол­жен быть про­пор­циона­лен количес­тву переза­писан­ных битов, то есть рас­сто­янию Хэм­минга меж­ду дву­мя зна­чени­ями HD(L1,L2).

Би­товое рас­сто­яние Хэм­минга HD(L1, L2) рав­но весу Хэм­минга от сум­мы по модулю двух этих перемен­ных HW(L1 xor L2), дру­гими сло­вами: HD(L1, L2) = HW(L1 xor L2). Имея в рас­поряже­нии исходные тек­сты, мы можем най­ти зна­чение это­го выраже­ния по фор­муле на рис. 8. В этой фор­муле все парамет­ры, кро­ме клю­ча K1, могут быть най­дены из исходно­го тек­ста, поэто­му мы лег­ко можем смо­дели­ровать количес­тво перек­лючений битов в регис­тре L, ког­да L1 переза­писы­вает L2.

Те­оре­тичес­ки мы можем рас­счи­тать любую дру­гую переза­пись регис­тров, нап­ример L4 и L5, но в этом слу­чае фор­мула будет содер­жать зна­чение клю­чей от K1 до K4 и нам будет очень слож­но искать ключ по час­тям. С дру­гой сто­роны, мож­но ата­ковать пос­ледние раун­ды и вос­поль­зовать­ся шиф­ротек­ста­ми, как мы делали это для алго­рит­ма AES, — нуж­но лишь написать обратные опе­рации InvSbox, InvP, InvE.

Фор­мула на рис. 8 абсо­лют­но пра­виль­ная, но ужас­но неудоб­ная, потому что мы собира­емся модели­ровать шесть бит клю­ча, которые пода­ются на вход Sbox, а выход собирать нам при­дет­ся из раз­ных мест, так как перес­танов­ка P переме­шива­ет все выходы. На мой взгляд, это ужас­но неудоб­но, но есть эле­ган­тное решение проб­лемы. Побито­вая перес­танов­ка P не изме­няет вес Хэм­минга, поэто­му если мы при­меним обратную перес­танов­ку InvP, то вес Хэм­минга тоже не поменя­ется. Эта фор­мула при­веде­на на рис. 9.

Та­кая фор­мула гораз­до удоб­нее, так как поз­воля­ет еди­нож­ды пос­читать опе­рацию InvP(R0 xor L0), а затем для каж­дого зна­чения клю­ча прос­то брать выход Sbox и счи­тать перек­лючение битов (индексы над перемен­ными озна­чают, какие биты нуж­но взять, что­бы сос­тавить модель для пер­вых шес­ти бит клю­ча). Если это пре­обра­зова­ние тебе не очень ясно, то прос­то вос­поль­зуйся фор­мулой на рис. 8, но не забудь пра­виль­но «сло­вить» биты пос­ле перес­танов­ки P.

Оче­вид­но, ты уже понял, как искать ключ. Прос­то переби­рая все зна­чения шес­ти бит клю­ча, вна­чале рас­счи­тыва­ешь модель пот­ребле­ния энер­гии. Затем счи­таешь кор­реляцию меж­ду моделью и реаль­ными дан­ными, и луч­шее зна­чение кор­реляции даст тебе вер­ный ключ. С кодом нуж­но будет чуть‑чуть повозить­ся.

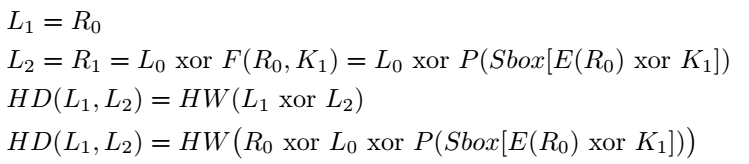
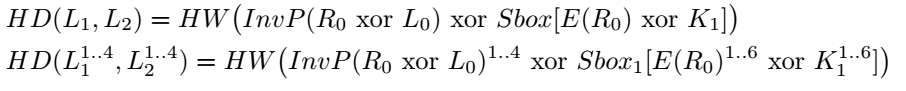
Шаг 5. Разбираемся с кодом

Что­бы упростить задачу, я вос­поль­зовал­ся реали­заци­ей DES, выпол­ненной Жу­аном Фран­ко (Joao Franco). Вна­чале мы рас­счи­таем все зна­чения, которые не изме­няют­ся со сме­ной клю­ча, то есть зна­чения E(R0) и InvP(L0 xor R0), обоз­начен­ные в коде (рис. 10) в качес­тве ER0 и InvL0R0. Для рас­чета исполь­зовалась реали­зация Жуана Фран­ко и допол­нитель­ная таб­лица обратной перес­танов­ки InvPFtable. Пос­ле вычис­ления про­межу­точ­ных зна­чений мы можем прис­тупить к пос­тро­ению самих моделей, как это сде­лано в коде на рис. 11. Пос­ле того как будет выпол­нен весь код (а это зай­мет некото­рое вре­мя), у тебя дол­жен получить­ся гра­фик, при­веден­ный на рис. 12. Сре­ди всех гра­фиков здесь есть один, у которо­го кор­реляция зна­читель­но отли­чает­ся в момент 10-го так­та с начала работы. Это говорит о том, что модель для одно­го из клю­чей хорошо сог­ласу­ется с реаль­ными дан­ными и, ско­рее все­го, ключ пра­виль­ный. На это так­же кос­венно ука­зыва­ет момент кор­реляции — если бы пик был в дру­гой такт, то это бы про­тиво­речи­ло нашей модели, которая опи­рает­ся на переза­пись регис­тра пос­ле вто­рого раун­да.

Нем­ного изме­няя код ,ты самос­тоятель­но можешь пос­тро­ить кор­реляции для оставших­ся час­тей клю­ча. Так­же ты можешь попытать­ся про­ата­ковать пос­ледний раунд, для это­го соз­дай модель, ког­да R15 переза­писы­вает­ся зна­чени­ем R16. Если будут воп­росы, то пиши на ука­зан­ный в начале адрес.

Шаг 6. Подведем итог

В этот раз статья сфо­куси­рова­на на том, что­бы поз­волить тебе самос­тоятель­но «пощупать» реаль­но изме­рен­ные дан­ные. Если пред­став­ленно­го фай­ла тебе мало — на сай­те DPA contest есть око­ло 12 Гб раз­личных дан­ных, которые мож­но про­ана­лизи­ровать. За три статьи мы разоб­рали осно­вы атак по вто­рос­тепен­ным каналам, и, начиная со сле­дующей статьи, мы зай­мем­ся ата­ками методом инду­циро­ван­ных сбо­ев. Затем, ког­да прой­дет нем­ного вре­мени, мы вер­немся к ата­кам по вто­рос­тепен­ным каналам, но уже будем рас­смат­ривать слож­ные и еще более приб­лижен­ные к реаль­нос­ти при­меры. А пока у тебя есть воз­можность поиг­рать­ся с дан­ными и поис­кать допол­нитель­ную информа­цию в Сети или в стать­ях жур­нала «Хакер». Stay tuned!