Криптография: time-based атаки на хеши

Криптография воспринимается как волшебная палочка, по мановению которой любая информационная система становится защищенной. Но на удивление криптографические алгоритмы могут быть успешно атакованы. Все сложные теории криптоанализа нивелируются, если известна малейшая информация о промежуточных значениях шифра. Помимо ошибок в реализации, получить такую информацию можно, манипулируя или измеряя физические параметры устройства, которое выполняет шифр, и я постараюсь объяснить, как это возможно.

Откуда растут рога

Давай попробуем рассмотреть реализацию любого криптографического алгоритма сверху вниз. На первом этапе криптографический алгоритм записывается в виде математических операторов. Здесь алгоритм находится в среде, где действуют только законы математики, поэтому исследователи проверяют лишь математическую стойкость алгоритма, или криптостойкость. Этот шаг нас интересует мало, ибо математические операции должны быть переведены в код. На этапе работы кода критическая информация о работе шифра может утекать через лазейки в реализации. Переполнение буфера, неправильная работа с памятью, недокументированные возможности и другие особенности программной среды позволяют злоумышленнику найти секретный ключ шифра без использования сложных математических выкладок. Многие останавливаются на этом шаге, забывая, что есть еще как минимум один. Данные — это не абстракция, а реальное физическое состояние логических элементов, в то время как вычисления — это физические процессы, которые переводят состояние логических элементов из одного в другое. Следовательно, выполнение программы — это преобразование физических сигналов, и с такой точки зрения результат работы алгоритма определяется законами физики. Таким образом, реализация криптографического алгоритма может рассматриваться в математической, программной и физической средах.

В конечном счете любой алгоритм выполняется с помощью аппаратных средств, под которыми понимаются любые вычислительные механизмы, способные выполнять логические операции И, ИЛИ и операцию логического отрицания. К ним относятся стандартные полупроводниковые устройства, такие как процессор и ПЛИС, нейроны мозга, молекулы ДНК и другие. У всех вычислительных средств есть как минимум два общих свойства. Первое свойство — для того, чтобы выполнить вычисление, нужно затратить энергию. В случае полупроводниковых устройств мы говорим об электрической энергии, в случае нейронов мозга, вероятно, о затраченных калориях (видел когда-нибудь толстых шахматистов?), в случае ДНК это, к примеру, химические реакции с выделением теплоты. Второе общее свойство в том, что для корректного выполнения операций все вычислительные механизмы требуют нормальных внешних условий. Полупроводниковые устройства нуждаются в постоянном напряжении и токе, нейроны мозга в покое (пробовал вести машину, когда твоя девушка пытается выяснить отношения?), ДНК в температуре. На этих двух свойствах основаны аппаратные атаки (hardware attacks), о которых пойдет речь.

На первый взгляд кажется, что физические процессы абсолютно нерелевантны с точки зрения безопасности, но это не так. Энергию, которая была израсходована в данный конкретный момент работы алгоритма, можно измерить и связать с двоичными данными, которые позволят найти ключ шифрования. На измерении физических эффектов, протекающих во время вычислений, основаны все атаки, которые называются атаки по второстепенным каналам (Side Channel Attacks). В России этот термин еще не до конца устоялся, поэтому можно встретить словосочетания «атаки по побочным каналам», «атаки по сторонним каналам» и другие.

Нормальные внешние условия тоже являются немаловажными. Рассмотрим, к примеру, напряжение, которое необходимо подать на вход процессора. Что случится, если это напряжение упадет до нуля на несколько наносекунд? Как может показаться на первый взгляд, процессор не перезагрузится, но, скорее всего, континуум физических процессов будет нарушен и результат алгоритма будет неверным. Создав ошибку в нужный момент, злоумышленник может вычислить ключ, сравнивая правильный и неправильный шифротексты. Изменение внешних условий используется для вычисления ключей в атаках по ошибкам вычислений (Fault attacks). Опять же в России этот термин устоялся не полностью: называют их и атаками с помощью ошибок, и атаками методом индуцированных сбоев, и по-другому.

Атаки по второстепенным каналам

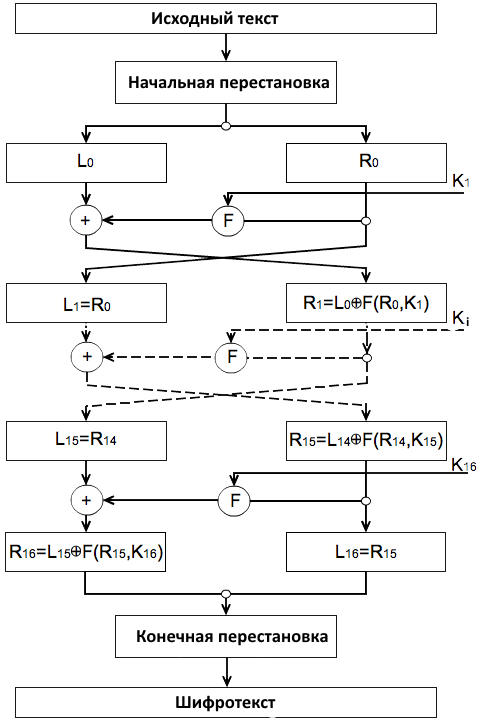
Мы начнем введение в атаки по второстепенным каналам с алгоритма DES, реализованного на C++ (схема алгоритма представлена на рис. 1, а его подробное описание ищи в Сети). Помимо того что ты увидишь, в каких неожиданных местах могут скрываться уязвимости, ты также узнаешь про основные приемы, используемые в атаках по второстепенным каналам. Эти приемы необходимо прочувствовать, так как они служат основой для более сложных атак, которые будут рассмотрены в последующих статьях.

Атаки по времени

Итак, атака по времени (Timing attack) на реализацию алгоритма DES. Полный код будет ждать тебя на dvd.xakep.ru, нас же в данный момент интересует побитовая перестановка Р (ищи круг с буквой Р на рис. 2), выполняемая на последнем шаге блока Файстеля. В нашем случае код этой функции выполнен следующим образом:

#define GETBIT(x,i) ((x>>(i)) & 0x1)

uint8_t p_tab[32] = {16,7,20,21,29,12,28,17,1,15,23,26,5,18,31,10,2,8,24,14,32,27,3,9,19,13,30,6,22,11,4,25};

uint32_t DES_P(const uint32_t var){

    int iBit = 0;

    uint32_t res = 0x0, one = 0x1;

    for (iBit=0; iBit<32; iBit++)

        if (GETBIT(var,32 - p_tab[iBit]) == 1)

            res |= one<<(31-iBit);

    return res;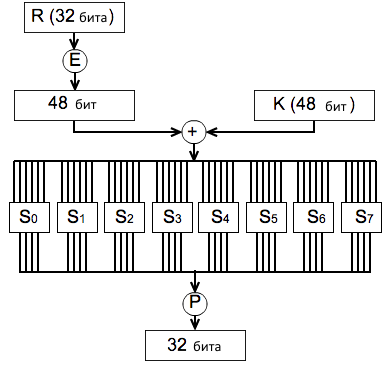

}

С точки зрения аппаратных атак этот код содержит гигантскую уязвимость: программа будет выполнять операцию res |= one<<(31-iBit), то есть затрачивать дополнительное время (читай энергию), только если бит переменной var равен 1. Переменная var, в свою очередь, зависит от исходного текста и ключа, поэтому, связав время работы программы со значением ключа, мы получим инструмент для атаки. Чтобы понять, как использовать связь между временем и данными, я рассмотрю два теоретических примера. Затем в третьем примере будет показано, как непосредственно найти ключ алгоритма, использующего данную реализацию.

Сравнение ключей при идеальных измерениях

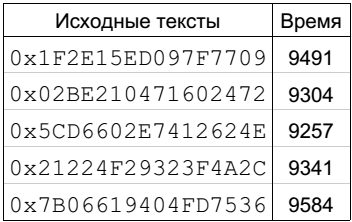
Первый теоретический пример заключается в том, что у нас есть пять исходных текстов, идеально измеренное время шифрования каждого текста и два ключа: К1=0x3030456789ABCDEF, К2=0xFEDCBA9876540303, из которых нужно выбрать правильный. Мы полагаем, что код не прерывался во время выполнения, данные были заранее размещены в кеше первого уровня, а время работы всех функций шифра за исключением функции DES_P было постоянным. Замечу, что шифротекстов нет, поэтому зашифровать один исходный текст с помощью двух ключей и сравнить получившиеся шифротексты с оригиналом не получится. Что в этом случае можно сделать?

Ты уже знаешь, что переменная var влияет на время работы, которое содержит две составляющие:

• переменное время, затрачиваемое на выполнение всех операций DES_P, которое зависит от количества бит переменной var для каждого раунда: a*(∑HW(var)), где

- `а` — это постоянная времени, фактически это количество тактов процессора, затраченных на выполнение одной операции `res |= one<<(31-iBit)`;

- `HW(var)` — расстояние Хемминга, то есть количество бит переменной `var`, установленных в 1. Знак суммы `∑` означает, что мы считаем расстояние Хемминга для всех 16 раундов;

• постоянное время, затрачиваемое на выполнение всех остальных операций, будет обозначено Т.

Следовательно, время работы всего алгоритма равно t = a*(∑HW(var)) + T. Параметры a и T нам неизвестны, и, сразу тебя обрадую, искать мы их не будем. Время шифрования каждого исходного текста t мы измерили идеально. Также у нас есть значения ключей, поэтому мы можем рассчитать переменную var для каждого раунда.

Я думаю, ты уже догадался, как проверить, какой из двух ключей правильный: нужно рассчитать сумму расстояний Хемминга ∑HW(var) для каждого исходного текста и одного значения ключа и сравнить получившиеся значения с измеренным временем. Очевидно, что с ростом значения ∑HW(var) время также должно увеличиваться. Следовательно, если ключ правильный, то такая зависимость будет прослеживаться, а вот для неправильного ключа такой зависимости не будет.

Все вышесказанное можно записать в виде одной таблицы (рис. 3).

В первой колонке у нас находятся исходные тексты, которые шифруются с помощью одного из ключей К1 или К2 (какого конкретно — нужно узнать). Во второй колонке — время, указанное в процессорных тактах, которое было затрачено на шифрование одного исходного текста. В третьей колонке находятся суммы значений расстояний Хемминга переменной var для всех раундов, полученные для каждого исходного текста и ключа К1. В четвертой колонке такая же сумма расстояний Хемминга, но уже посчитанная для ключа К2. Как несложно заметить, время работы шифра увеличивается с ростом значений расстояний Хемминга для ключа К1. Соответственно, ключ К1 будет верным.

Конечно, это идеализированный пример, который не учитывает множество факторов, возникающих в реальности. Я хотел показать лишь примерный принцип атак по второстепенным каналам, а вот уже следующий пример будет объяснен на реально измеренных значениях времени, но перед этим нужно вспомнить кое-что из статистики.

Угадай число

Мне хотелось бы показать, что происходит со случайными величинами, когда они очень долго усредняются. Если ты хорошо знаешь статистику, то сразу переходи к следующей части, в противном случае давай рассмотрим небольшую игру, где компьютер случайно выбирает натуральное число А и предлагает тебе угадать его. Каждый раз компьютер выбирает дополнительную пару чисел (b, c) из диапазона от 0 до М и возвращает тебе лишь значения (А + b, c). Числа b и с выбираются случайно и могут быть значительно больше числа А. Значение числа М ты не знаешь (но можешь примерно догадаться о его порядке из-за разброса значений c). Как угадать число А?

Программа, которая симулирует эту игру, приведена ниже:

void Game(int *Ab, int *с){

    static int A = 0;

    int M = 1000;

    srand((unsigned int)rdtsc());

    if (A==0)

        A = 1+rand()%100;

    *Ab = A+(M*M*rand())%M;

    *с = (M*M*rand())%M;

}

void Guess(){

    int Ab, с, i, nTries = 100000;

    double avg1 = 0.0, avg2 = 0.0;

    for (i=0; i<nTries; i++){

        Game(&Ab, &c);

        avg1 += Ab;

        avg2 += c;

    }

    printf("%f\n", roundf((avg1-avg2)/numTries));

}

Согласно коду, значение А берется из диапазона от 1 до 100, а значения переменных b и с из диапазона от 0 до 999, что примерно в десять раз больше максимального значения А, то есть уровень шума значительно выше уровня самого значения! Но если пара значений (А + b, с) возвращается 100 тысяч раз (много, но и уровень шума тоже не маленький), то значение переменной А угадывается примерно в половине случаев. Для этого нужно усреднить все возвращенные значения А + b и все значения с, а затем посчитать разность средних. Эта разность и будет значением переменной А. Конечно, если мы уменьшим значение М, то и количество пар (A + b, с), необходимых для вычисления ключа, будет меньшим.

Теперь нужно разобраться, почему так происходит. Существует замечательный закон, который является ключевым для атак по второстепенным каналам, — закон больших чисел Чебышева. Согласно этому закону, при большом числе независимых опытов среднее арифметическое наблюденных значений μ(x) случайной величины x сходится по вероятности к ее математическому ожиданию. Если рассматривать этот закон в рамках нашей игры, сумма значений A + b и c сойдется соответственно к А + μ(b) и μ(c), а так как значения b и c выбираются случайно из одного диапазона, то μ(b) и μ(c) будут сходиться к их математическому ожиданию, следовательно, разность А + μ(b) – μ(c) будет сходиться к значению переменной А.

Сравнение ключей при реальных измерениях

Прерывания, кеширование данных и другие факторы не позволяют измерить время работы алгоритма с точностью до одного процессорного такта. В моих измерениях время работы алгоритма варьируется в пределах 5% от среднего значения. Этого достаточно, чтобы метод из первого примера перестал работать.

Что можно придумать в этом случае? Сразу замечу, что одним лишь усреднением времени шифрования каждого исходного текста решить задачу не получится (хотя время будет измерено точнее). Во-первых, это далеко не всегда возможно, так как входные значения шифра могут контролироваться не нами. Во-вторых, даже усреднив миллион шифрований, ты не избавишься от проблемы кеширования данных, так как разместить все таблицы в кеше первого уровня сложно (ну по крайней мере об этом нужно позаботиться заранее), — о таких особенностях я расскажу как-нибудь в следующий раз.

Теперь рассмотрим, как влияет закон больших чисел Чебышева на атаки по второстепенным каналам. Мы все так же рассматриваем реализацию DES, но сейчас время работы алгоритма записывается следующим образом:

• переменное время, затрачиваемое на выполнение операции DES_P, которое зависит от количества бит переменной var: a*(∑HW(var)). а по-прежнему постоянная времени, а HW(var) — расстояние Хемминга;

• постоянное время, затрачиваемое на выполнение всех остальных Т;

• шумы измерений Δ(t), которые нормально распределены в диапазоне [0:D]. Значение D неизвестно, и, как всегда, искать его мы не будем.

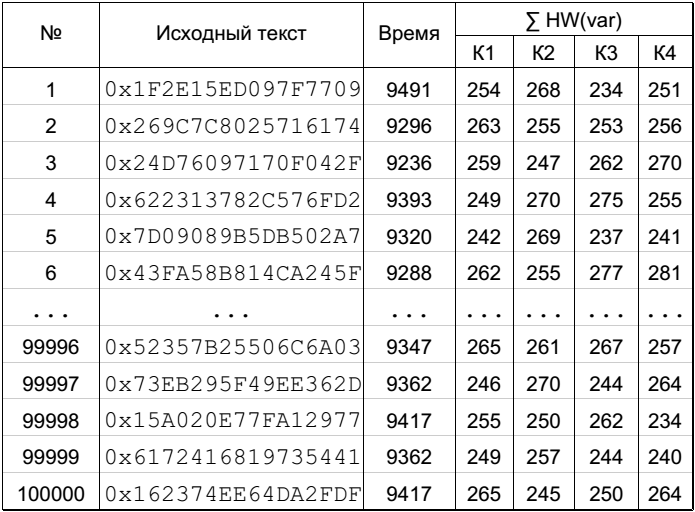
Таким образом, время работы алгоритма можно записать в виде t = a*(∑HW(var)) + T + Δ(t). В таблице, представленной на рис. 4, приведены значения исходных текстов и реально измеренное время для них. Замечу, что ∑HW(var) для правильного ключа и каждого исходного текста равно 254, но при этом разница между наименьшим и наибольшим временем составляет 327 тактов!

При таких вариациях в измерениях простое попарное сравнение расстояний Хемминга для одного исходного текста и времени его шифрования не даст результатов. Здесь мы должны воспользоваться законом больших чисел Чебышева. Что случится, если мы будем усреднять время алгоритма для разных шифротекстов, которые дают одинаковое расстояние Хемминга ∑HW(var):

μ(t) = μ(a*(∑HW(var)) + T + Δ(t)) = μ(a*(∑HW(var))) + μ(T) + μ(Δ(t)) = a*(∑HW(var)) + T + μ(Δ(t))

Фактически, когда определяется среднее арифметическое времени для различных исходных текстов, происходит усреднение шумов, и, как мы знаем из статистики, эти шумы будут сходиться к одному и тому же значению при увеличении количества измерений, то есть μ(Δ(t)) будет сходиться к константе.

Давай посмотрим на примере. Я измерил работу 100 тысяч операций шифрования алгоритма DES, то есть у меня есть 100 тысяч исходных текстов и соответствующих времен работы. В этот раз мы будем сравнивать четыре ключа: К1=0x3030456789ABCDEF, K2=0xFEDCBA9876540303, K3=0x2030456789ABCDEF, K4=0x3030456789ABCDED. Как и в первом примере, мы рассчитываем значение расстояний Хемминга для всех исходных текстов и ключей К1,К2,К3,К4 — это сделано в таблице, представленной на рис. 5. Ни для одного из ключей нет очевидной зависимости времени от расстояний Хемминга.

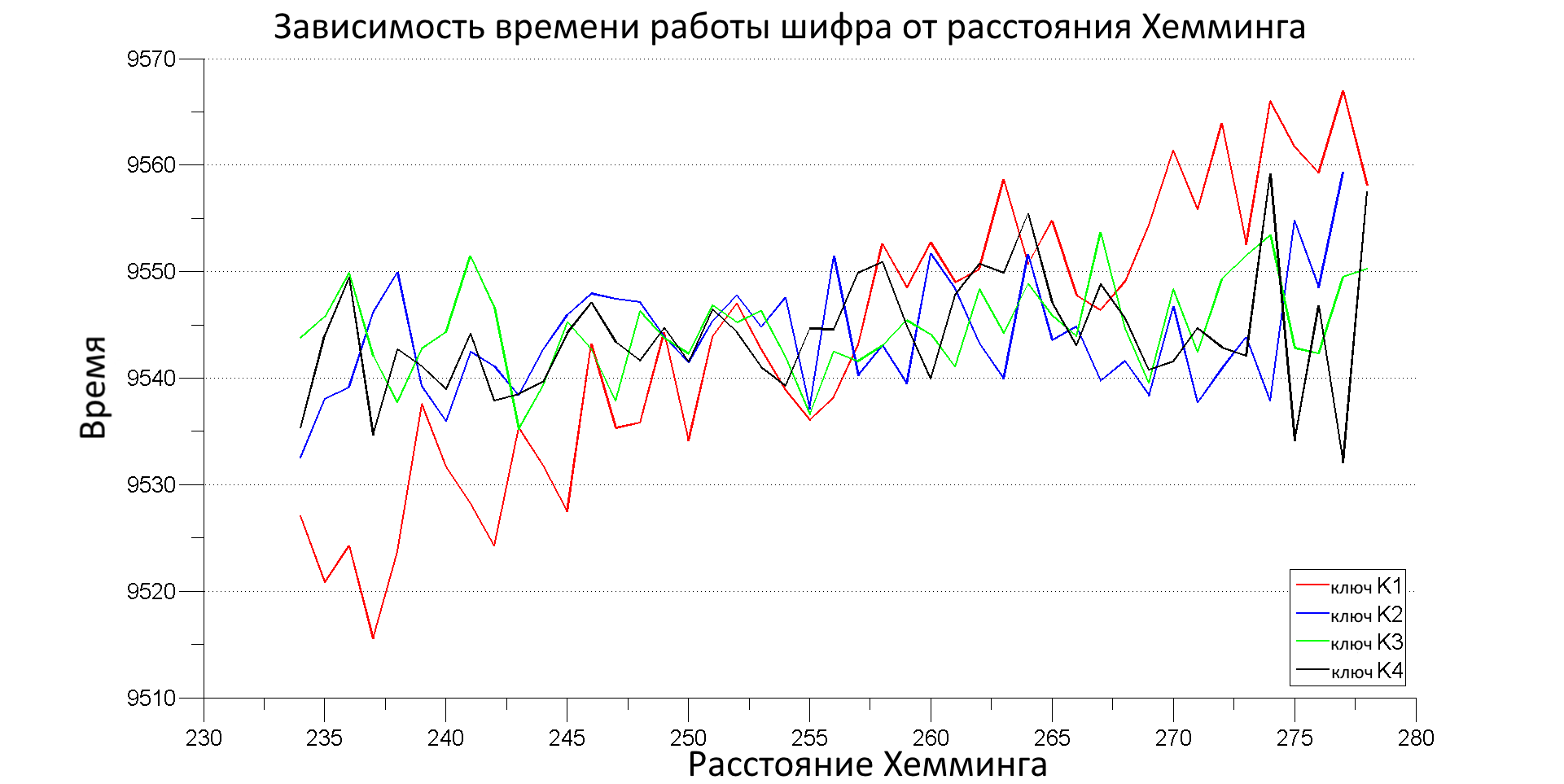
Давай усредним время работы шифрований (для каждого ключа по отдельности), у которых одно и то же расстояние Хемминга (возьмем лишь те исходные тексты, для которых ∑HW(var) лежит в интервале [234,276]). В этот раз мы построим график (рис. 6), где по оси Х будет отложено расстояние Хемминга, а по оси Y — среднее арифметическое времени для этого расстояния.

Коэффициент корреляции Пирсона

Что мы видим на рис. 6? Для трех ключей (К2, К3, К4) время работы шифра слабо зависит от расстояния Хемминга, а для ключа К1 мы видим восходящий тренд. Обрати внимание на пилообразный вид графиков — это из-за того, что у нас не так много измерений и они не настолько точные, чтобы μ(Δ(t)) усреднилось к одному значению. Все же мы можем видеть, что среднее время работы шифра увеличивается с ростом расстояний Хемминга, посчитанных для ключа К1, а для трех других ключей — нет. Поэтому предполагаем, что ключ К1 верный (это действительно так). С ростом количества данных восходящий тренд для правильного ключа будет разве что усиливаться, а для неправильных ключей все значения будут сходиться к среднему. «Гребенка» тоже будет исчезать с ростом количества данных.

Согласись, строить такие графики и постоянно проверять их глазами довольно неудобно, для этого есть несколько стандартных тестов проверки зависимости между моделью и реальными данными: коэффициент корреляции, Т-тест и взаимная информация. Можно вспомнить и придумать еще парочку других коэффициентов, но мы будем в основном пользоваться коэффициентом корреляции Пирсона или, что то же самое, линейным коэффициентом корреляции pcc(x,y) (описание коэффициента есть на Wiki). Этот коэффициент характеризует степень линейной зависимости между двумя переменными. В нашем случае зависимость именно линейная, ибо μ(t) = a*(∑HW(var)) + T + μ(Δ(t)) можно представить как y = a*x + b, где x — это рассчитываемое нами расстояние Хемминга, а y — реально измеренное время. Значение коэффициента корреляции Пирсона для средних значений времени и расстояний Хемминга показано в строке «с усреднением» на рис. 7.

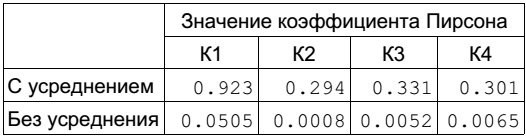
Значение коэффициента Пирсона для ключа К1 в три раза выше, чем для любого из трех других ключей. Это говорит о высоком линейном соответствии между моделируемыми и реальными данными, что лишний раз подтверждает использование ключа К1.

Коэффициент корреляции Пирсона можно применять даже без предварительного усреднения значений. В этом случае его величина будет существенно меньше, чем для усредненных значений, но все равно правильный ключ будет давать наибольший коэффициент корреляции (строка «без усреднения»).

Таким образом, вначале визуально, а затем с помощью коэффициента корреляции мы смогли убедиться, что наша модель времени для ключа К1 лучше всего согласуется с реальными данными. Очевидно, что проверять все возможные значения основного ключа не представляется возможным, поэтому нам необходим другой метод, который позволит искать ключ по частям. Такой метод приводится в следующем примере, который уже можно рассматривать как применимую в жизни атаку.

Атака на неизвестный ключ

Вот мы и подошли к моменту, когда ключ будет искаться частями по 6 бит. Искать 6 бит мы будем абсолютно аналогично тому, как проверяли корректность 64 бит до этого (когда работали с четырьмя ключами). Значения 6 бит ключа, которые дают самую хорошую линейную связь между моделью и реальными данными, скорее всего, будут правильными. Как это работает?

Давай рассмотрим, как можно представить время работы шифра, когда мы ищем лишь 6 бит ключа:

• переменное время, затрачиваемое на выполнение операции DES_P, зависящее от:

- 4 бит переменной `var` первого раунда `a*HW(var[1,1:4])` (6 бит ключа первого раунда участвуют в формировании 4 бит переменной `var`);

- всех остальных бит переменной `var` за исключением 4 бит первого раунда `a*(∑ HW(var[:,1:32]))`;

• постоянное время Т;

• шумы измерений Δ(t).

Таким образом, время работы алгоритма можно записать в виде

t = a*HW(var[1,1:4]) + a*(∑ HW(var[:,1:32])) + Т + Δ(t). 

Еще раз по поводу 6 бит ключа и 4 бит переменной var. Блок Файстеля берет 32 бита регистра R и с помощью специальной перестановки E() получает 48 бит, которые затем складываются с 48 битами ключа. На первом раунде значение R нам известно, а ключ нет. Далее результат сложения разбивается (внимание!) на восемь блоков по 6 бит, и каждый набор из 6 бит подается на свою собственную таблицу Sbox. Каждая из восьми таблиц заменяет шесть входных бит четырьмя выходными битами, поэтому на выходе получается 32-битная переменная var, которая уже влияет на время работы шифра.

Если мы сгруппируем время работы всех операций шифрования, для которых расстояние Хемминга HW(var[1,1:4]) одинаковое, то среднее арифметическое времени работы будет сходиться к следующему значению:

μ(t) = μ(a*HW(var[1,1:4])) + μ(a*(∑ HW(var[:,1:32]))) + μ(Т) + μ(Δ(t)) = a*HW(var[1,1:4]) +  μ(a*(∑ HW(var[:,1:32]))) + Т + μ(Δ(t)). 

Так как мы берем одинаковые значения HW(var[1,1:4]) и разные значения ∑ HW(var[:,1:32]) (мы берем исходные тексты, где HW(var[1,1:4]) обязательно одинаковое, а остальные части нас не интересуют, поэтому суммы ∑ HW(var[:,1:32]) будут разные), то среднее арифметическое μ(a*(∑ HW(var[:,1:32]))) будет сходиться к константе (если совсем точно, то μ(∑ HW(var[:,1:32])) без учета первых четырех бит должна сходиться к 254), точно так же, как в предыдущем примере сходилась величина μ(Δ(t))!

Первые четыре бита переменной var можно записать как var[1,1:4] = Sbox{E(R)[1,1:6] xor K[1,1:6]}, где E(R)[1,1:6] — первые 6 бит регистра R после операции E(); K[1,1:6] — первые 6 бит ключа; Sbox{} — таблица перестановки Sbox. Теперь заменим выражение для var[1,1:4]:

μ(t) = a*HW(Sbox{E(R)[1,1:6] xor K[1,1:6]}) +  μ(a*(∑ HW(var[:,1:32]))) + Т + μ(Δ(t)). 

Значения μ(a*(∑ HW(var[:,1:32]))), μ(Δ(t)) сходятся к своим средним арифметическим, когда они считаются для разных исходных текстов. Следовательно, при очень большом количестве усреднений значение μ(a*(∑ HW(var[:,1:32]))) + Т + μ(Δ(t)) можно просто заменить на const:

μ(t) = a*HW(Sbox{E(R)[1,1:6] xor K[1,1:6]}) +  const.

Чтобы найти ключ в этом выражении, нужно для каждого значения 6 бит ключа выбрать исходные тексты с одинаковым HW(Sbox{E(R)[1,1:6] xor K[1,1:6]}), усреднить их время выполнения и сравнить с моделью. Окончательный алгоритм поиска ключа запишем в виде псевдокода:

For each key = 0:63

    For each i = 1:N

        P = plaintext(i) // Исходный текст

        [L, R] = IP(P) // Левая и правая части после начальной перестановки

        hw_var[i] = HammingWeight( Sbox1(E(R)[0:5] XOR key) ) // Расстояние Хемминга для первых четырех бит переменной var

    EndFor

    // Коэффициент корреляции между N измеренными значениями времени и N посчитанными значениями расстояния Хемминга

    pcc(key) = ComputePearsonCorrelation(t, hw_var) 

EndFor

Этот алгоритм был реализован на С++ (полный исходный код будет ждать тебя на dvd.xakep.ru), и посчитанные коэффициенты корреляции показаны на рис. 8. Для расчета корреляции был использован миллион измерений. Комбинации битов ключа 000010=2 дает корреляцию в четыре раза выше, чем для любого другого значения, поэтому, скорее всего, эта комбинация битов является верной. Замечу, что мы ищем ключ первого раунда, который не равен изначальному ключу.

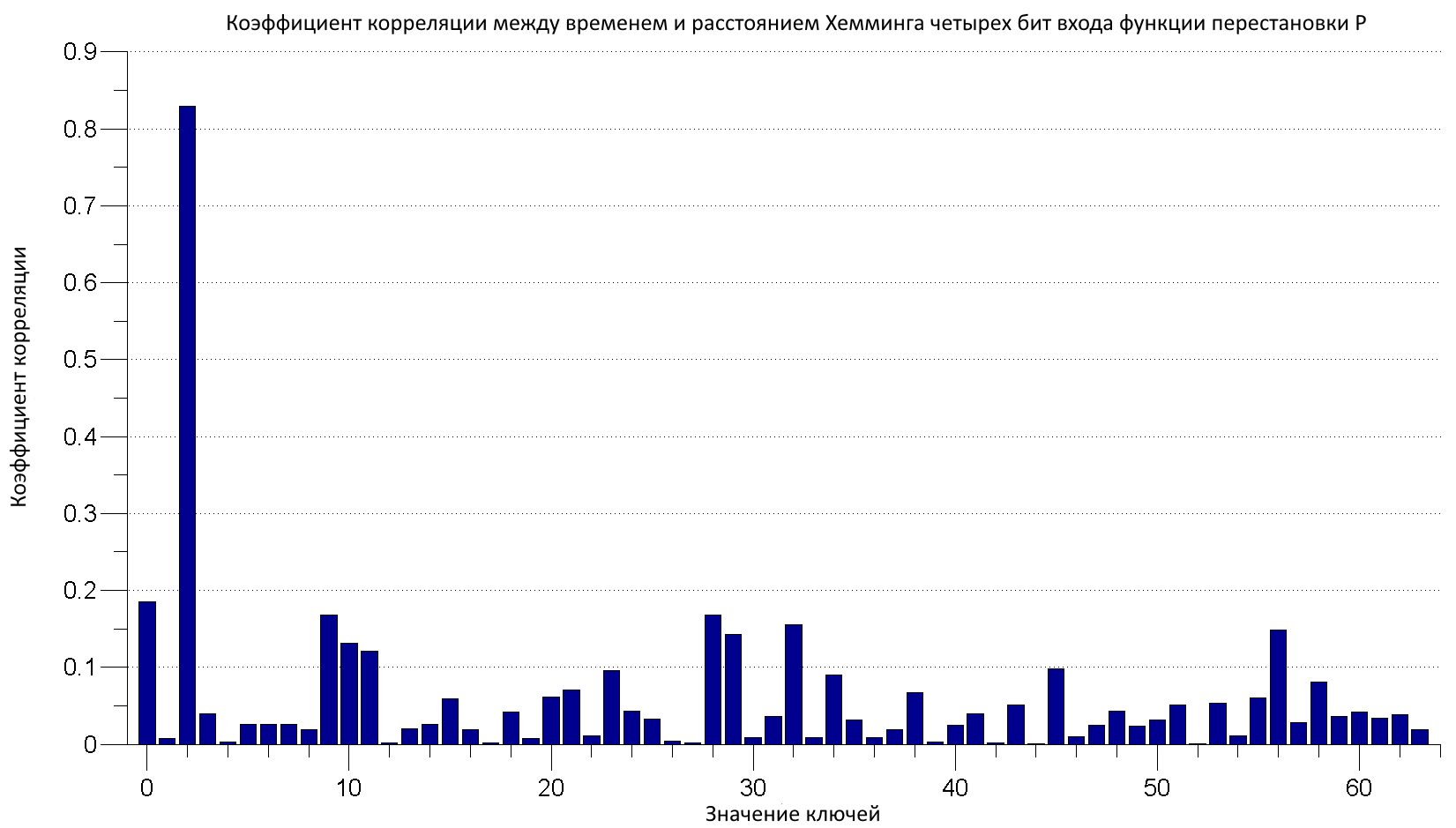
После того как были найдены первые 6 бит ключа, можно искать следующие, пока ключ не будет восстановлен полностью. Сбор значений времени может занимать от нескольких часов до нескольких недель в зависимости от системы. Анализ данных обычно происходит значительно быстрее — за несколько часов, хотя тоже зависит от ситуации. Коммерческого ПО для атак по времени в открытом доступе нет, но ты всегда можешь воспользоваться моими исходниками.

Продолжение следует

Пришло время закругляться. Первая статья всегда комом, ибо она может показаться легкой/непрактичной/неинтересной, но без вводной части далеко не уйдешь. Ну а в последующих номерах журнала мы продолжим изучение аппаратных атак, разберем, как воспользоваться потребленным питанием устройства, чтобы взломать шифр, и как восстановить ключ с помощью ошибок в вычислениях. Так что stay tuned, как говорят.