Мозги напрокат. Как сделать нейросеть или воспользоваться чужой

Нейросети сейчас в моде, и не зря. С их помощью можно, к примеру, распознавать предметы на картинках или, наоборот, рисовать ночные кошмары Сальвадора Дали. Благодаря удобным библиотекам простейшие нейросети создаются всего парой строк кода, не больше уйдет и на обращение к искусственному интеллекту IBM.

Теория

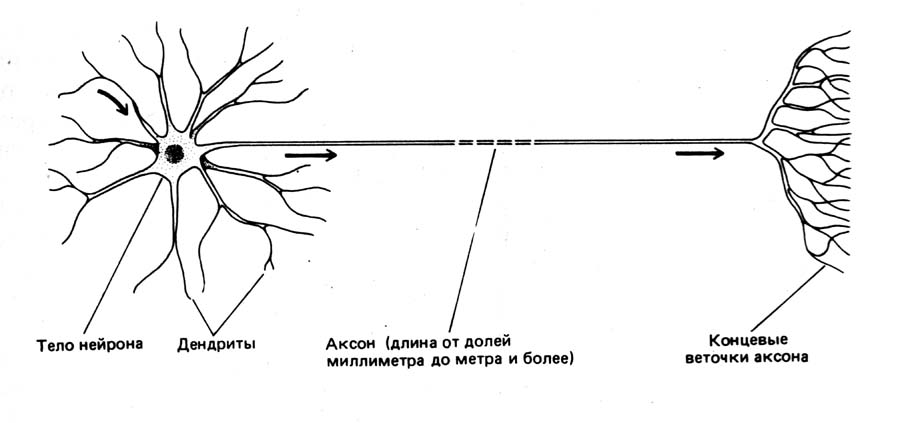
Биологи до сих пор не знают, как именно работает мозг, но принцип действия отдельных элементов нервной системы неплохо изучен. Она состоит из нейронов — специализированных клеток, которые обмениваются между собой электрохимическими сигналами. У каждого нейрона имеется множество дендритов и один аксон. Дендриты можно сравнить со входами, через которые в нейрон поступают данные, аксон же служит его выходом. Соединения между дендритами и аксонами называют синапсами. Они не только передают сигналы, но и могут менять их амплитуду и частоту.

Преобразования, которые происходят на уровне отдельных нейронов, очень просты, однако даже совсем небольшие нейронные сети способны на многое. Все многообразие поведения червя Caenorhabditis elegans — движение, поиск пищи, различные реакции на внешние раздражители и многое другое — закодировано всего в трех сотнях нейронов. И ладно черви! Даже муравьям хватает 250 тысяч нейронов, а то, что они делают, машинам определенно не под силу.

Почти шестьдесят лет назад американский исследователь Фрэнк Розенблатт попытался создать компьютерную систему, устроенную по образу и подобию мозга, однако возможности его творения были крайне ограниченными. Интерес к нейросетям с тех пор вспыхивал неоднократно, однако раз за разом выяснялось, что вычислительной мощности не хватает на сколько-нибудь продвинутые нейросети. За последнее десятилетие в этом плане многое изменилось.

Вот в двух словах, как работает нейросеть. Искусственный нейрон, как и настоящий, имеет несколько входов и один выход. У каждого входа есть весовой коэффициент. Меняя эти коэффициенты, мы можем обучать нейронную сеть. Зависимость сигнала на выходе от сигналов на входе определяет так называемая функция активации.

В перцептроне Розенблатта функция активации складывала вес всех входов, на которые поступила логическая единица, а затем сравнивала результат с пороговым значением. Ее минус заключался в том, что незначительное изменение одного из весовых коэффициентов при таком подходе способно оказать несоразмерно большое влияние на результат. Это затрудняет обучение.

В современных нейронных сетях обычно используют нелинейные функции активации, например сигмоиду. К тому же у старых нейросетей было слишком мало слоев. Сейчас между входом и выходом обычно располагают один или несколько скрытых слоев нейронов. Именно там происходит все самое интересное.

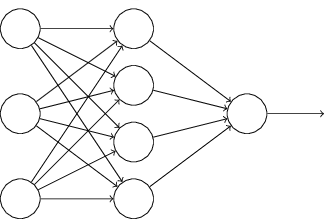
Чтобы было проще понять, о чем идет речь, посмотри на эту схему. Это нейронная сеть прямого распространения с одним скрытым слоем. Каждый кружок соответствует нейрону. Слева находятся нейроны входного слоя. Справа — нейрон выходного слоя. В середине располагается скрытый слой с четырьмя нейронами. Выходы всех нейронов входного слоя подключены к каждому нейрону первого скрытого слоя. В свою очередь, входы нейрона выходного слоя связаны со всеми выходами нейронов скрытого слоя.

Не все нейронные сети устроены именно так. Например, существуют (хотя и менее распространены) сети, у которых сигнал с нейронов подается не только на следующий слой, как у сети прямого распространения с нашей схемы, но и в обратном направлении. Такие сети называются рекуррентными. Полностью соединенные слои — это тоже лишь один из вариантов, и одной из альтернатив мы даже коснемся.

Практика

Итак, давай попробуем построить простейшую нейронную сеть своими руками и разберемся в ее работе по ходу дела. Мы будем использовать Python с библиотекой Numpy (можно было бы обойтись и без Numpy, но с Numpy линейная алгебра отнимет меньше сил). Рассматриваемый пример основан на коде Эндрю Траска.

Нам понадобятся функции для вычисления сигмоиды и ее производной:

import numpy

def sigmoid(x):
  return 1/(1+numpy.exp(-x))

def deriv(x):
  return x*(1-x)

Роль Hello World в мире машинного обучения играет распознавание рукописных цифр по набору данных MNIST, состоящему из 60 тысяч образцов почерка, но для наших целей это, увы, слишком. Мы займемся кое-чем попроще: попробуем найти зависимость между тремя входными значениями и одним выходным. Вот набор данных для обучения сети:

X = numpy.array([[0,0,1], [0,1,1], [1,0,1], [1,1,1]])
y = numpy.array([[0], [1], [1], [0]])

Наша сеть будет устроена в точности так же, как на картинке: входной слой с тремя нейронами, скрытый слой с четырьмя и выходной слой с одним. Каждая связь между нейронами (или, как говорят биологи, каждый синапс) имеет весовой коэффициент. Мы будем хранить их в матрицах syn1 и syn2: первая соответствует связям между входным и скрытым слоем, вторая — между скрытым и выходным.

Исходные значения весовых коэффициентов случайны. Небольшое пояснение для тех, кто незнаком с Numpy: пара чисел, переданная numpy.random.random, определяет размерность матрицы, которая будет создана и заполнена случайными числами:

syn0 = 2*numpy.random.random((3, 4)) - 1
syn1 = 2*numpy.random.random((4, 1)) - 1

Приготовления закончены, и можно перейти к делу. Остаток кода заключен в цикл, который повторится 60 тысяч раз, пока мы обучаем сеть.

l0 — это матрица, описывающая входной слой сети. Он совпадает с исходными данными. l1 соответствует скрытому слою сети. Чтобы узнать его значения, мы перемножаем значения нейронов входного слоя (l0) и вес соединений между входным и скрытым слоем (syn0), а затем пропускаем результаты через сигмоидную функцию. l2 соответствует выходному слою сети. Он считается по тому же принципу, но с l1 вместо l0 и с syn1 вместо syn0. Вычисления происходят слева направо: от входа к скрытому слою, а от скрытого слоя — к выходному:

for j in xrange(60000):
  l0 = X
  l1 = sigmoid(numpy.dot(l0, syn0))
  l2 = sigmoid(numpy.dot(l1, syn1))

Значения, которые сохранены в l2, — это сделанное нейронной сетью на основе входных данных предсказание результата. На первых порах его значение, скорее всего, будет заметно отличаться от нужного. Чтобы исправить это, мы должны пройти в обратном направлении, от выхода к входу, и скорректировать вес соединений в соответствии с ошибкой.

Сначала сравним результаты (l2) с целевыми значениями (y), а затем подготовимся к корректировке весовых коэффициентов. Значения в l2_delta зависят от «уверенности» в соответствующих им результатах. Высокая уверенность ведет к маленьким значениям и, соответственно, минимальному изменению весового коэффициента:

l2_error = y - l2
l2_delta = l2_error*deriv(l2)

Повторим этот процесс для скрытого слоя (l1). Значения итоговых ошибок достигают его не без потерь. Поскольку вклад нейронов скрытого слоя в ошибку зависел от веса соединений (syn1), ошибка тоже пересчитывается с учетом весовых коэффициентов:

l1_error = l2_delta.dot(syn1.T)
l1_delta = l1_error * deriv(l1)

Остается шаг, на котором, собственно говоря, и происходит обучение. Пересчитываем вес для каждого соединения:

syn1 += l1.T.dot(l2_delta)
syn0 += l0.T.dot(l1_delta)

Вот и все. Если бы слоев было больше, ошибка так и переходила бы от слоя к слою, уменьшаясь в соответствии с весом соединений по мере приближения к старту. Это называют обратным распространением ошибки (backpropagation).

Очевидно, что наш подход к программированию многослойных нейронных сетей, основанный преимущественно на операции copy-paste, не особенно практичен. По-хорошему, сначала следовало бы позаботиться об абстракциях, а еще лучше — не изобретать велосипед и поинтересоваться, не позаботились ли о них другие.

Даже если брать во внимание только Python, существует множество готовых библиотек, предназначенных для реализации нейронных сетей и других алгоритмов машинного обучения. Хороший пример — библиотека Pybrain, сводящая описание и обучение простой сети к трем строкам:

network = buildNetwork(dataset.indim, 4, dataset.outdim)
t = BackpropTrainer(network, learningrate = 0.01, momentum = 0.99)
t.trainOnDataset(dataset, 60000)

Суть описанного понятна без дополнительных объяснений. Это, к слову, редкость: для освоения наиболее мощных программных средств, доступных в этой области, требуются изрядные усилия.

Опасное погружение

Слово «глубинный» в модном термине «глубинное обучение», который несколько лет назад вызвал всплеск интереса к нейронным сетям, намекает на использование сетей с большим количеством скрытых слоев. Предполагается, что при анализе данных каждый следующий слой будет извлекать из них все более и более абстрактные особенности.

Поскольку наша конечная цель — распознавание изображений, давай поговорим о сверточных нейронных сетях. Это относительно новая разновидность нейронных сетей, которая особенно эффективна именно для распознавания изображений.

У нейронной сети с полностью соединенными слоями, которую мы рассматривали выше, входы каждого нейрона скрытого слоя соединены с выходами всех нейронов входного слоя. В сверточной сети это не так. Тут нейроны скрытого слоя соединены лишь с небольшой выборкой нейронов входного слоя, причем каждый со своей.

Это значит, что если сеть работает с изображениями и нейроны входного слоя соответствуют его пикселям, то каждый нейрон скрытого слоя будет получать информацию лишь о небольшом участке изображения — например, фрагменте пять на пять пикселей. Участки соседних нейронов пересекаются, а все вместе они полностью покрывают картинку.

И это еще не все. Весовые коэффициенты соответствующих связей и смещение (показатель, зависящий от порогового значения) каждого нейрона сверточного слоя полностью совпадают. По сути дела, все нейроны слоя действуют как единственный нейрон, который рассматривает картинку через очень маленькое окошко со всех возможных сторон сразу.

Набор общих весовых коэффициентов и смещение обычно называют фильтром. Фильтр предназначен для выявления одного признака — скажем, границы между объектами на изображении или, например, определенной текстуры. Поскольку одного признака, как правило, мало, у одного слоя, занимающегося сверткой, может быть несколько фильтров — по одному на распознаваемый признак.

За сверточным слоем обычно следует слой субдискретизации (pooling), упрощающий полученные результаты. Этого можно достичь по-разному, но нередко изображение, образованное результатами свертки, просто делят на клетки и находят максимальное значение для каждой из них (max pooling). Информация о том, где именно был найден признак, при этом теряется, но она на этом этапе уже не играет роли. Важнее сам факт, что признак найден, и положение этого признака относительно других. Комбинация сверточного слоя и слоя субдискретизации часто повторяется несколько раз и увенчивается полностью соединенным слоем, интегрирующим информацию со всего изображения.

Пример простой сверточной сети есть все в том же Pybrain, а убедиться в том, что она неплохо распознает изображения, можно при помощи примера classify_image.py, прилагающегося к мощной библиотеке TensorFlow, которую разработали в Google. Этот пример использует сеть, обученную на миллионах изображений из базы данных ImageNet. Необходимые для ее работы данные скрипт автоматически скачивает при первом запуске.

$ python classify_image.py --image_file cow.jpg

Эту сеть натренировали делить изображения по содержанию на тысячу типов, и это очень специфическая тысяча. classify_image.py прекрасно разбирается в экзотических животных, но ничего не знает о людях. Если продемонстрировать программе фотографию коровы, она задумается на несколько секунд, а потом предположит, что это вол или бык.

Это еще куда ни шло, а вот понимание кадра, на котором запечатлены Путин и Медведев, далось гугловской нейронной сети с трудом. Она заметила на фото мужской костюм (уверенность — 64%), галстучный узел (5%) и новобрачных (4%). В качестве демонстрации возможностей не так уж плохо, но для того, чтобы использовать эту программу на практике, потребуется существенная доработка.

Мозги напрокат

Времена, когда для распознавания образов нужно было становиться специалистом по машинному обучению, похоже, подходят к концу. Несколько месяцев назад компания Google объявила о начале закрытого бета-тестирования веб-сервиса Google Cloud Vision API, к которому можно будет программно обратиться для того, чтобы выяснить содержание картинки, выделить на ней отдельные объекты и лица или прочитать надписи.

Аналогичный сервис AlchemyAPI, разработанный в IBM, функционирует уже пару лет. Чтобы начать им пользоваться, достаточно зарегистрироваться на alchemyapi.com и получить ключ разработчика. Программный интерфейс построен в стиле REST: каждой функции соответствует отдельный URL на сервере gateway-a.watsonplatform.net, аргументы передаются HTTP-вызовом, а результаты приходят в ответ в виде XML или JSON.

Испытаем удачу с уже проверенными картинками. Для классификации изображений в AlchemyAPI предусмотрено две функции: URLGetRankedImageKeywords и ImageGetRankedImageKeywords. Они отличаются лишь тем, каким образом передается изображение — в виде ссылки или в виде файла по POST. Мы воспользуемся первым вариантом — он проще:

def call_api(endpoint, **kwargs):
  request = urllib2.Request(endpoint, urllib.urlencode(kwargs))
  return json.load(urllib2.urlopen(request))

>>> pprint.pprint(call_api('http://gateway-a.watsonplatform.net/calls/url/URLGetRankedImageKeywords', url='http://goo.gl/I9ytWA', apikey=apikey, outputMode='json'))

{u'imageKeywords': [{u'score': u'0.985226', u'text': u'animal'},
                    {u'score': u'0.964429', u'text': u'cow'},
                    {u'score': u'0.598688', u'text': u'cattle'},
                    {u'score': u'0.5',      u'text': u'farm'}],
u'status': u'OK',}

Корову AlchemyAPI разглядел идеально (процитированная выше выдача немного сокращена). С Путиным детище IBM было менее многословно: оно сообщило лишь, что на картине люди. Для того чтобы разбираться с людьми, служат другие функции: URLGetRankedImageFaceTags и ImageGetRankedImageFaceTags. Попробуем скормить президента им:

>>> pprint.pprint(call_api('http://gateway-a.watsonplatform.net/calls/url/URLGetRankedImageFaceTags', url='http://goo.gl/Jh34qd', apikey=apikey, outputMode='json'))

Ответ выдается в формате JSON и хорошо структурирован. Сервис IBM не только нашел на картинке людей и определил их пол и возраст, но и сообразил, кто это такие: Владимир Путин, по его мнению, — это политик, телевизионный актер и мастер боевых искусств, а Дмитрий Медведев — политик и президент. Не поспоришь!

Бесплатно можно делать до тысячи запросов к AlchemyAPI в сутки. Дальше придется платить, но тарифы терпимы: до 0,75 цента за одно обращение к сервису. Не такая уж большая плата за то, чтобы не утруждать собственные нейроны. Они, говорят, не восстанавливаются.