Содержание статьи
В одной из статей, посвященных отечественной криптографии, мы разобрались, как применять блочные криптоалгоритмы «Кузнечик» и «Магма» для шифрования сообщений, размер которых превышает размер одного блока (для «Кузнечика» он составляет 16 байт, а для «Магмы» — 8 байт) с использованием режима простой замены (ECB, от английского Electronic Codebook). Этот режим описан в ГОСТ 34.13—2015 «Информационная технология. Криптографическая защита информации. Режимы работы блочных шифров». Этот нормативный документ, помимо режима простой замены, определяет еще несколько способов применения блочных шифров, а именно:
- режим гаммирования (CTR, от английского Counter);
- режим гаммирования с обратной связью по выходу (OFB, от английского Output Feedback);
- режим простой замены с зацеплением (CBC, от английского Cipher Block Chaining);
- режим гаммирования с обратной связью по шифртексту (CFB, от английского Cipher Feedback);
- режим выработки имитовставки (MAC, от английского Message Authentication Code).
Что ж, давай разберемся, как работает гаммирование и как его применять на практике.
INFO
В настоящее время ГОСТ 34.12—2015 и ГОСТ 34.13—2015 обрели статус межгосударственных (в рамках нескольких государств СНГ) и получили наименования соответственно ГОСТ 34.12—2018 и ГОСТ 34.13—2018. Оба стандарта введены в действие в качестве национальных стандартов Российской Федерации с 1 июня 2019 года.
Общие принципы реализации режима гаммирования
Гамма шифра
Гаммирование — это наложение (или снятие при расшифровке сообщений) на открытое (или зашифрованное) сообщение так называемой криптографической гаммы. Криптографическая гамма — это последовательность элементов данных, которая вырабатывается с помощью определенного алгоритма. Наложение (или снятие) гаммы на блок сообщения в рассматриваемом нами стандарте реализуется с помощью операции побитного сложения по модулю 2 (XOR). То есть при шифровании сообщений каждый блок открытого сообщения ксорится с блоком криптографической гаммы, длина которого должна соответствовать длине блоков открытого сообщения. При этом, если размер блока исходного текста меньше, чем размер блока гаммы, блок гаммы обрезается до размера блока исходного текста (выполняется процедура усечения гаммы).
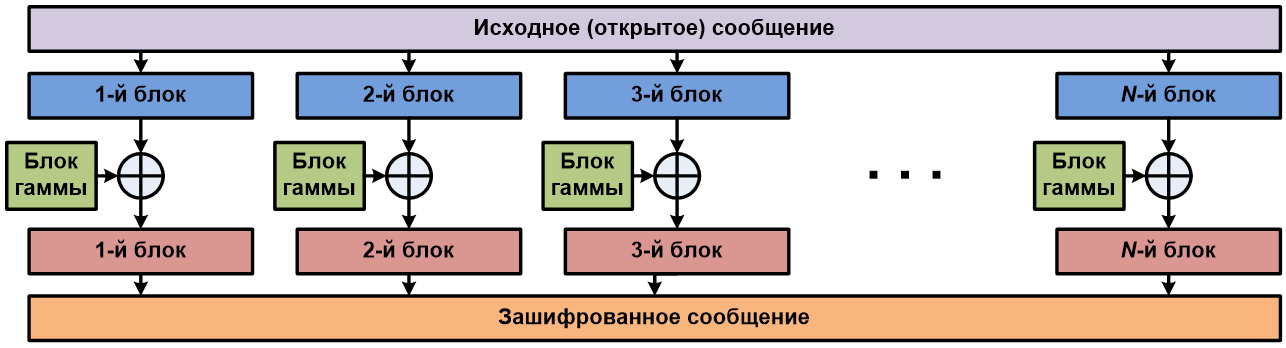
Для дешифровки закрытого сообщения необходимо произвести обратную операцию. То есть каждый блок зашифрованного сообщения ксорится с блоком гаммы, и на выходе мы имеем требуемое расшифрованное сообщение.
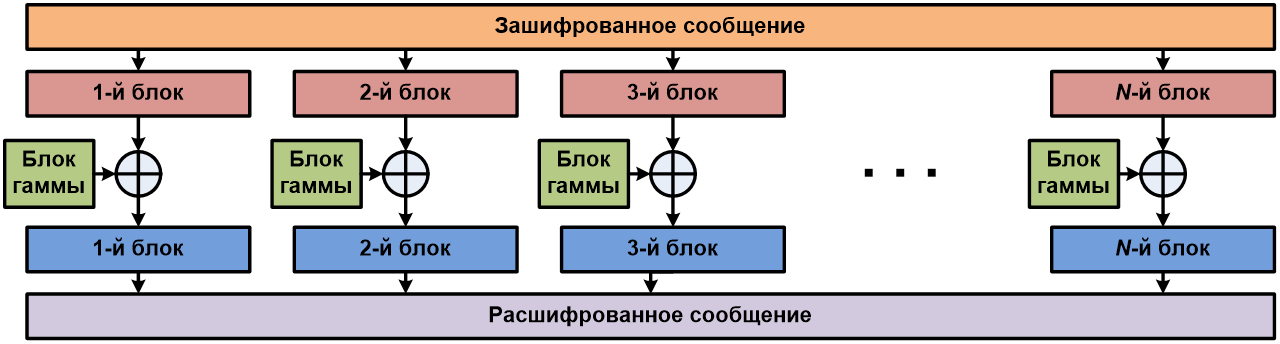
В большинстве случаев размер блока исходного текста принимается равным размеру блока используемого алгоритма блочного шифрования (напомню, это 16 байт при использовании алгоритма «Кузнечик» или 4 байт при использовании «Магмы»), поэтому процедура усечения блока гаммы может понадобиться только для последнего блока исходного текста, в случае, когда общая длина сообщения не кратна размеру одного блока и последний блок получается неполный.
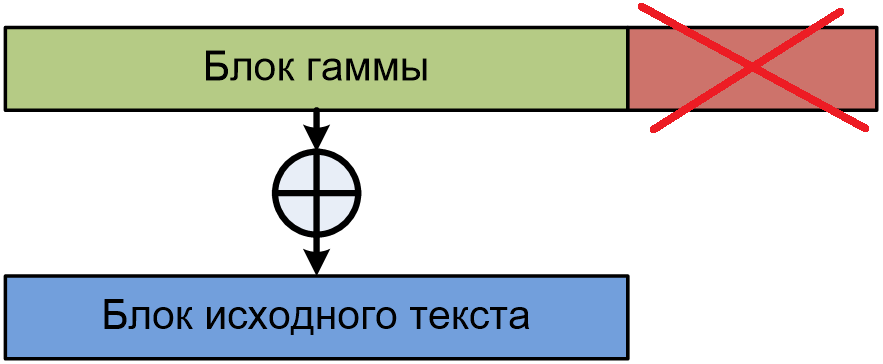
Чтобы обеспечить высокую стойкость шифрования, блоки гаммы должны отличаться друг от друга, а также иметь случайный (или псевдослучайный) характер. В данном случае блоки различаются благодаря так называемому инициализирующему вектору, значение которого меняется от блока к блоку. Псевдослучайность блоков гаммы при этом реализуется путем шифрования этого вектора с использованием выбранного алгоритма (мы используем «Магму»).
Инициализирующий вектор
Значение этого вектора формируется из так называемой синхропосылки, которая представляет собой число определенной длины. Для режима гаммирования длина этого числа должна быть равна половине размера одного блока используемого алгоритма блочного шифрования. Само значение синхропосылки для режима гаммирования должно быть уникальным для каждого цикла шифрования, проведенного с использованием одинаковых ключей, при этом требований к конфиденциальности синхропосылки не предъявляется (то есть ее можно передавать в открытом виде вместе с зашифрованным сообщением).
В режиме гаммирования инициализирующий вектор формируется дополнением нулями синхропосылки до размера одного блока используемого алгоритма блочного шифрования. В случае «Магмы» длина синхропосылки равна четырем байтам, длина инициализирующего вектора — восьми. Вторая часть инициализирующего вектора (заполненная нулями) будет использоваться в качестве того самого счетчика (Counter), который и лег в основу англоязычного сокращения CTR.
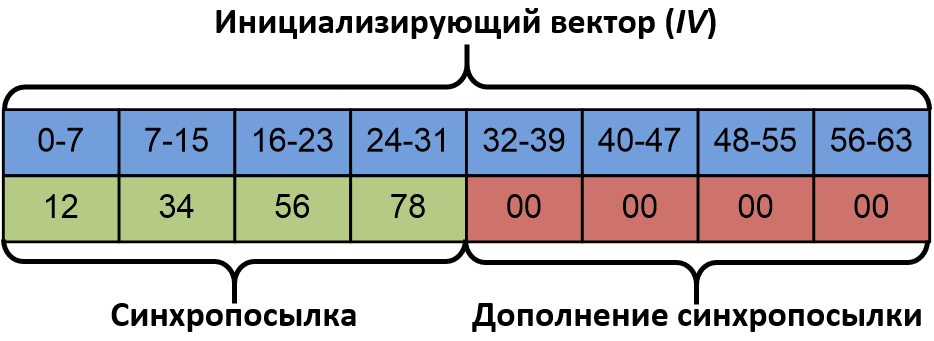
Очередной блок гаммы шифра получается благодаря шифрованию значения счетчика (его начальное значение равно инициализирующему вектору) с помощью выбранного алгоритма блочного шифрования, при этом после выработки очередного блока гаммы значение счетчика увеличивается на единицу.

Продолжение доступно только участникам
Вариант 1. Присоединись к сообществу «Xakep.ru», чтобы читать все материалы на сайте
Членство в сообществе в течение указанного срока откроет тебе доступ ко ВСЕМ материалам «Хакера», позволит скачивать выпуски в PDF, отключит рекламу на сайте и увеличит личную накопительную скидку! Подробнее
Вариант 2. Открой один материал
Заинтересовала статья, но нет возможности стать членом клуба «Xakep.ru»? Тогда этот вариант для тебя! Обрати внимание: этот способ подходит только для статей, опубликованных более двух месяцев назад.
Я уже участник «Xakep.ru»


