Содержание статьи
Четыре слона отечественной криптографии
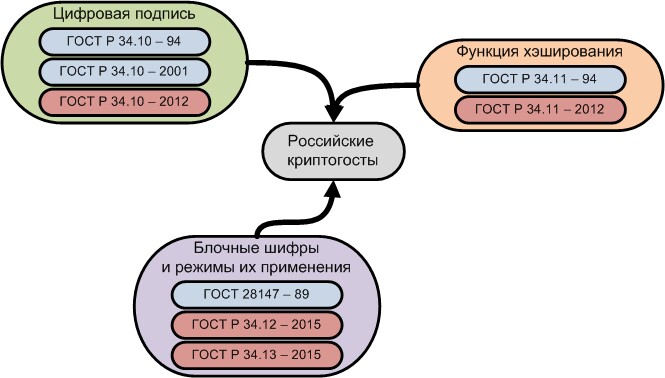
В настоящее время отечественная криптография базируется на нескольких основных государственных стандартах:
- ГОСТ 34.10. Информационная технология. Криптографическая защита информации. Процессы формирования и проверки электронной цифровой подписи (действующая на сегодня редакция 2012 года);
- ГОСТ 34.11. Информационная технология. Криптографическая защита информации. Функция хэширования (действующая на сегодня редакция 2012 года);
- ГОСТ 34.12. Информационная технология. Криптографическая защита информации. Блочные шифры (действующая на сегодня редакция 2015 года);
- ГОСТ 34.13. Информационная технология. Криптографическая защита информации. Режимы работы блочных шифров (действующая на сегодня редакция 2015 года).
С ГОСТ 34.11—2012 мы уже познакомились в прошлой статье цикла. Это, если помнишь, был алгоритм вычисления хеш-суммы под названием «Стрибог». Сегодня мы продолжим рассматривать отечественную криптографию, и на очереди у нас алгоритм блочного шифрования под названием «Кузнечик», который описан в ГОСТ 34.12—2015.
Как и положено, данный ГОСТ разработан в научных недрах российских спецслужб и близко к ним стоящих организаций, а если говорить конкретнее, то это Центр защиты информации и специальной связи ФСБ России и открытое акционерное общество «Информационные технологии и коммуникационные системы». Документ вступил в силу с 1 января 2016 года, и все средства шифрования, официально используемые в различных структурах, работающих с информацией ограниченного доступа (гостайна, служебная тайна и прочее), должны ему соответствовать.
В стандарте описываются две разновидности блочного шифра: «Кузнечик» с длиной блока 128 бит и «Магма» с длиной блока 64 бита.
Алгоритм «Кузнечик» более современный и теоретически более стойкий, чем алгоритм «Магма» (который, по сути, практически без изменений был взят из старого ГОСТ 28147—89), и поэтому сегодня мы рассмотрим именно его. Что касается «Магмы», то о нем — как-нибудь в другой раз в следующей статье цикла.
Как уже было сказано, длина шифруемого блока в алгоритме «Кузнечик» — 128 бит. Длина ключа шифрования — 256 бит.
WARNING
При чтении ГОСТа учти, что во всех 16-байтовых массивах тестовых последовательностей нулевой байт находится в конце массива, а пятнадцатый, соответственно, в начале (если ты внимательно читал статью про «Стрибог», то эта особенность наших криптостандартов тебе должна быть знакома).
INFO
Одна из главных легенд российской криптографии гласит, что название алгоритма «Кузнечик» никакого отношения к зеленому насекомому не имеет, а представляет собой сокращение от фамилий создателей алгоритма — Кузнецова и Нечаева. Скорее всего, это действительно так, хотя нигде официального подтверждения этому я найти не смог.
Немного теории
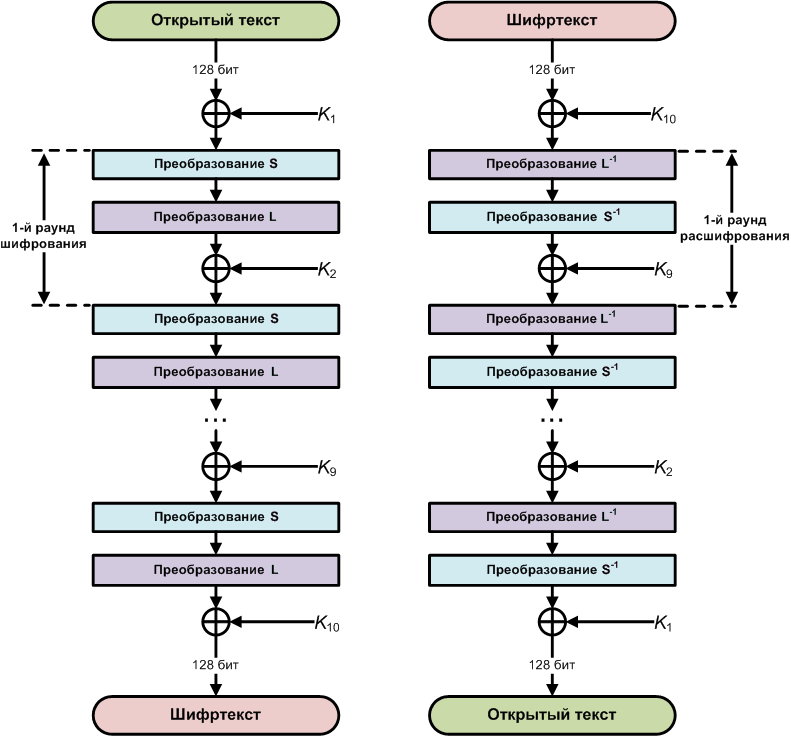
Основу алгоритма составляет не сеть Фейстеля, как в большинстве блочных шифров, а так называемая SP — Substitution-Permutation network, или, по-русски, подстановочно-перестановочная сеть. Шифр на основе SP-сети получает на вход блок и ключ и совершает несколько чередующихся раундов, состоящих из стадий подстановки и стадий перестановки. В «Кузнечике» каждый раунд включает в себя линейное и нелинейное преобразование плюс операцию наложения так называемого итерационного ключа. Всего таких раундов девять и один последний неполный раунд, в котором выполняется только наложение последнего (десятого) итерационного ключа.
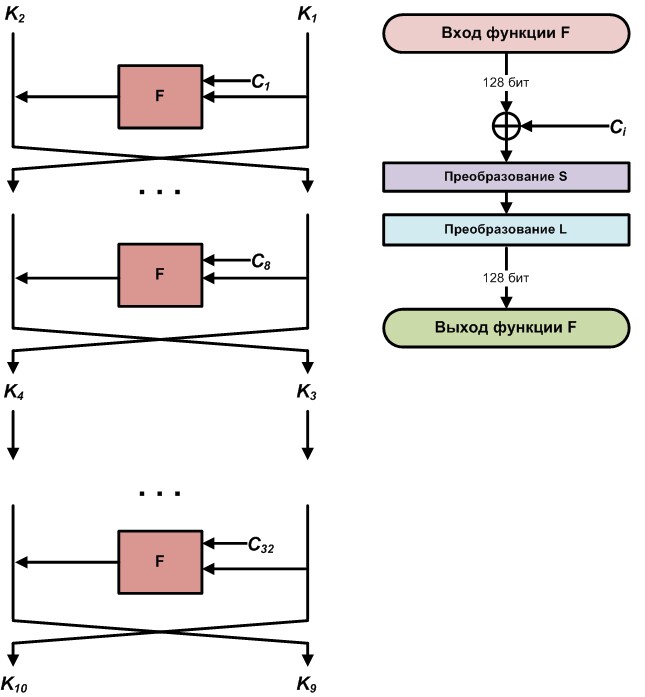
Итерационные (или раундовые) ключи получаются путем определенных преобразований на основе мастер-ключа, длина которого, как мы уже знаем, составляет 256 бит. Этот процесс начинается с разбиения мастер-ключа пополам, так получается первая пара раундовых ключей. Для генерации каждой последующей пары раундовых ключей применяется восемь итераций сети Фейстеля, в каждой итерации используется константа, которая вычисляется путем применения линейного преобразования алгоритма к значению номера итерации.
Итак, после краткого и небольшого погружения в теорию начинаем кодить...
Базовые функции стандарта
Поскольку в алгоритме используются 128-битные блоки (в виде так называемых двоичных векторов), для начала определим этот самый блок:
#define BLOCK_SIZE 16 // Размер блока 16 байт (или 128 бит)
...
typedef uint8_t vect[BLOCK_SIZE]; // Определяем тип vect как 16-байтовый массив
Сложение двух двоичных векторов по модулю 2
Данная функция в стандарте определена как X-преобразование. Каждый байт первого вектора ксорится с соответствующим байтом второго вектора, и результат пишется в третий (выходной) вектор:
static void GOST_Kuz_X(const uint8_t *a, const uint8_t *b, uint8_t *c)
{
int i;
for (i = 0; i < BLOCK_SIZE; i++)
c[i] = a[i] ^ b[i];
}
Нелинейное биективное преобразование (преобразование S)
Это преобразование в нашем случае повторяет S-преобразование из алгоритма «Стрибог» ГОСТ 34.11—2012. Массив S-преобразований тоже аналогичен ГОСТ 34.11—2012:
static const unsigned char Pi[256] = {
0xFC, 0xEE, 0xDD, ... 0x63, 0xB6
};
Здесь для экономии места показаны не все значения, определенные в стандарте, а только три первых и два последних. Когда будешь писать код, не забудь про остальные значения и про то, что в стандарте они записаны в десятичном виде.
Код самой функции преобразования S получается такой:
static void GOST_Kuz_S(const uint8_t *in_data, uint8_t *out_data)
{
int i;
for (i = 0; i < BLOCK_SIZE; i++)
out_data[i] = Pi[in_data[i]];
}

Обратное нелинейное биективное преобразование (обратное преобразование S)
Поскольку нам нужно не только зашифровывать сообщения, но и расшифровывать тоже, то каждому преобразованию зашифрования необходимо ставить в соответствие обратное преобразование для расшифрования. Сама функция обратного S-преобразования выглядит практически так же, как и прямое S-преобразование:
static void GOST_Kuz_reverse_S(const uint8_t *in_data, uint8_t *out_data)
{
int i;
for (i = 0; i < BLOCK_SIZE; i++)
out_data[i] = reverse_Pi[in_data[i]];
}
Отличие только в массиве преобразования, обратном к массиву прямого преобразования (в стандарте этот массив не приводится, поэтому напишем здесь его полностью):
static const unsigned char reverse_Pi[256] = {
0xA5, 0x2D, 0x32, 0x8F, 0x0E, 0x30, 0x38, 0xC0,
0x54, 0xE6, 0x9E, 0x39, 0x55, 0x7E, 0x52, 0x91,
0x64, 0x03, 0x57, 0x5A, 0x1C, 0x60, 0x07, 0x18,
0x21, 0x72, 0xA8, 0xD1, 0x29, 0xC6, 0xA4, 0x3F,
0xE0, 0x27, 0x8D, 0x0C, 0x82, 0xEA, 0xAE, 0xB4,
0x9A, 0x63, 0x49, 0xE5, 0x42, 0xE4, 0x15, 0xB7,
0xC8, 0x06, 0x70, 0x9D, 0x41, 0x75, 0x19, 0xC9,
0xAA, 0xFC, 0x4D, 0xBF, 0x2A, 0x73, 0x84, 0xD5,
0xC3, 0xAF, 0x2B, 0x86, 0xA7, 0xB1, 0xB2, 0x5B,
0x46, 0xD3, 0x9F, 0xFD, 0xD4, 0x0F, 0x9C, 0x2F,
0x9B, 0x43, 0xEF, 0xD9, 0x79, 0xB6, 0x53, 0x7F,
0xC1, 0xF0, 0x23, 0xE7, 0x25, 0x5E, 0xB5, 0x1E,
0xA2, 0xDF, 0xA6, 0xFE, 0xAC, 0x22, 0xF9, 0xE2,
0x4A, 0xBC, 0x35, 0xCA, 0xEE, 0x78, 0x05, 0x6B,
0x51, 0xE1, 0x59, 0xA3, 0xF2, 0x71, 0x56, 0x11,
0x6A, 0x89, 0x94, 0x65, 0x8C, 0xBB, 0x77, 0x3C,
0x7B, 0x28, 0xAB, 0xD2, 0x31, 0xDE, 0xC4, 0x5F,
0xCC, 0xCF, 0x76, 0x2C, 0xB8, 0xD8, 0x2E, 0x36,
0xDB, 0x69, 0xB3, 0x14, 0x95, 0xBE, 0x62, 0xA1,
0x3B, 0x16, 0x66, 0xE9, 0x5C, 0x6C, 0x6D, 0xAD,
0x37, 0x61, 0x4B, 0xB9, 0xE3, 0xBA, 0xF1, 0xA0,
0x85, 0x83, 0xDA, 0x47, 0xC5, 0xB0, 0x33, 0xFA,
0x96, 0x6F, 0x6E, 0xC2, 0xF6, 0x50, 0xFF, 0x5D,
0xA9, 0x8E, 0x17, 0x1B, 0x97, 0x7D, 0xEC, 0x58,
0xF7, 0x1F, 0xFB, 0x7C, 0x09, 0x0D, 0x7A, 0x67,
0x45, 0x87, 0xDC, 0xE8, 0x4F, 0x1D, 0x4E, 0x04,
0xEB, 0xF8, 0xF3, 0x3E, 0x3D, 0xBD, 0x8A, 0x88,
0xDD, 0xCD, 0x0B, 0x13, 0x98, 0x02, 0x93, 0x80,
0x90, 0xD0, 0x24, 0x34, 0xCB, 0xED, 0xF4, 0xCE,
0x99, 0x10, 0x44, 0x40, 0x92, 0x3A, 0x01, 0x26,
0x12, 0x1A, 0x48, 0x68, 0xF5, 0x81, 0x8B, 0xC7,
0xD6, 0x20, 0x0A, 0x08, 0x00, 0x4C, 0xD7, 0x74
};
Линейное преобразование (преобразование L)
Для выполнения данного преобразования необходима функция умножения чисел в конечном поле (или поле Галуа) над неприводимым полиномом x^8 + x^7 + x^6 + x + 1. Это самое сложное место для понимания в данном стандарте (даже Википедия не очень помогает). Реализуется это следующим образом:
static uint8_t GOST_Kuz_GF_mul(uint8_t a, uint8_t b)
{
uint8_t c = 0;
uint8_t hi_bit;
int i;
for (i = 0; i < 8; i++)
{
if (b & 1)
c ^= a;
hi_bit = a & 0x80;
a <<= 1;
if (hi_bit)
a ^= 0xc3; // Полином x^8 + x^7 + x^6 + x + 1
b >>= 1;
}
return c;
}
В целом, если внимательно посмотреть на код, можно увидеть, что это по большому счету умножение в столбик с добавлением числа 0xс3, которое и представляет нужный нам полином.
Далее, используя приведенную выше функцию, реализуем преобразование R, которое является частью линейного преобразования L. Преобразование R выполняется с использованием линейного регистра сдвига с обратной связью. Каждый байт из блока умножается с помощью функции GOST_Kuz_GF_Mul на один из коэффициентов из ряда (148, 32, 133, 16, 194, 192, 1, 251, 1, 192, 194, 16, 133, 32, 148, 1) в зависимости от порядкового номера байта. Байты складываются между собой по модулю 2, и все 16 байт блока сдвигаются в сторону младшего разряда, а полученное число записывается на место считанного байта.

Для реализации R-преобразования сначала определим массив нужных нам коэффициентов:
static const unsigned char l_vec[16] = {
1, 148, 32, 133, 16, 194, 192, 1,
251, 1, 192, 194, 16, 133, 32, 148
};
Далее пишем саму функцию R-преобразования:
static void GOST_Kuz_R(uint8_t *state)
{
int i;
uint8_t a_15 = 0;
vect internal;
for (i = 15; i >= 0; i--)
{
internal[i - 1] = state[i];// Двигаем байты в сторону младшего разряда
a_15 ^= GOST_Kuz_GF_mul(state[i], l_vec[i]);
}
// Пишем в последний байт результат сложения
internal[15] = a_15;
memcpy(state, internal, BLOCK_SIZE);
}
Линейное преобразование L образуется сдвигом регистра 16 раз, или шестнадцатикратным повторением функции GOST_Kuz_R:
static void GOST_Kuz_L(const uint8_t *in_data, uint8_t *out_data)
{
int i;
vect internal;
memcpy(internal, in_data, BLOCK_SIZE);
for (i = 0; i < 16; i++)
GOST_Kuz_R(internal);
memcpy(out_data, internal, BLOCK_SIZE);
}
Обратное линейное преобразование (обратное преобразование L)
Для того чтобы можно было не только зашифровывать сообщения, но и расшифровывать их, нам необходимо обратное линейное преобразование.
Это запишется следующим образом:
static void GOST_Kuz_reverse_L(const uint8_t *in_data, uint8_t *out_data)
{
int i;
vect internal;
memcpy(internal, in_data, BLOCK_SIZE);
for (i = 0; i < 16; i++)
GOST_Kuz_reverse_R(internal);
memcpy(out_data, internal, BLOCK_SIZE);
}
Как ты наверняка догадался, функция GOST_Kuz_reverse_R — это не что иное, как обратное преобразование R. Выглядит это таким образом:
static void GOST_Kuz_reverse_R(uint8_t *state)
{
int i;
uint8_t a_0;
a_0 = state[15];
vect internal;
for (i = 0; i < 16; i++)
{
internal[i] = state[i - 1];// Двигаем все на старые места
a_0 ^= GOST_Kuz_GF_mul(internal[i], l_vec[i]);
}
internal[0] = a_0;
memcpy(state, internal, BLOCK_SIZE);
}
Развертывание ключей
В начале мы уже говорили, что для зашифрования и расшифрования нам нужны десять итерационных ключей, а для их получения необходимы 32 итерационные константы, которые получаются из порядкового номера итерации с помощью L-преобразования.
Для начала определим место для хранения этих итерационных констант:
vect iter_C[32];// Итерационные константы C
Далее вычислим их:
vect iter_num[32];// Сюда будем писать номер итерации от 1 до 32
for (i = 0; i < 32; i++)
{
memset(iter_num[i], 0, BLOCK_SIZE);
iter_num[i][0] = i+1;
}
// Делаем преобразование L для каждого элемента массива iter_num
for (i = 0; i < 32; i++)
GOST_Kuz_L(iter_num[i], iter_C[i]);
Конечно, все это можно (и нужно, если ты хочешь, чтобы все работало немного быстрее) вычислить заранее и определить в тексте программы в виде констант. Мы же, чтобы соблюсти наглядность, пишем так, как показано в первоисточнике.
Далее определим функцию F, которая будет представлять одну итерацию развертывания ключа:
static void GOST_Kuz_F(const uint8_t *in_key_1, const uint8_t *in_key_2,
uint8_t *out_key_1, uint8_t *out_key_2,
uint8_t *iter_const)
{
vect internal;
memcpy(out_key_2, in_key_1, BLOCK_SIZE);
GOST_Kuz_X(in_key_1, iter_const, internal);
GOST_Kuz_S(internal, internal);
GOST_Kuz_L(internal, internal);
GOST_Kuz_X(internal, in_key_2, out_key_1);
}
На вход функции подаем очередную пару ключей, очередную итерационную константу, на выходе получаем промежуточную пару итерационных ключей.
Для того чтобы получить нужные нам десять итерационных (раундовых) ключей, нужно прокрутить функцию GOST_Kuz_F 32 раза. Но для начала определим место, где будут храниться полученные значения ключей:
vect iter_key[10]; // Итерационные ключи шифрования
После чего можно заняться непосредственным развертыванием ключей:
void GOST_Kuz_Expand_Key(const uint8_t *key_1, const uint8_t *key_2)
{
int i;
// Предыдущая пара ключей
uint8_t iter_1[64];
uint8_t iter_2[64];
// Текущая пара ключей
uint8_t iter_3[64];
uint8_t iter_4[64];
GOST_Kuz_Get_C(); // Вычисляем итерационные константы
// Первые два итерационных ключа равны паре мастер-ключа
memcpy(iter_key[0], key_1, 64);
memcpy(iter_key[1], key_2, 64);
memcpy(iter_1, key_1, 64);
memcpy(iter_2, key_2, 64);
for (i = 0; i < 4; i++)
{
GOST_Kuz_F(iter_1, iter_2, iter_3, iter_4, iter_C[0 + 8 * i]);
GOST_Kuz_F(iter_3, iter_4, iter_1, iter_2, iter_C[1 + 8 * i]);
GOST_Kuz_F(iter_1, iter_2, iter_3, iter_4, iter_C[2 + 8 * i]);
GOST_Kuz_F(iter_3, iter_4, iter_1, iter_2, iter_C[3 + 8 * i]);
GOST_Kuz_F(iter_1, iter_2, iter_3, iter_4, iter_C[4 + 8 * i]);
GOST_Kuz_F(iter_3, iter_4, iter_1, iter_2, iter_C[5 + 8 * i]);
GOST_Kuz_F(iter_1, iter_2, iter_3, iter_4, iter_C[6 + 8 * i]);
GOST_Kuz_F(iter_3, iter_4, iter_1, iter_2, iter_C[7 + 8 * i]);
memcpy(iter_key[2 * i + 2], iter_1, 64);
memcpy(iter_key[2 * i + 3], iter_2, 64);
}
}
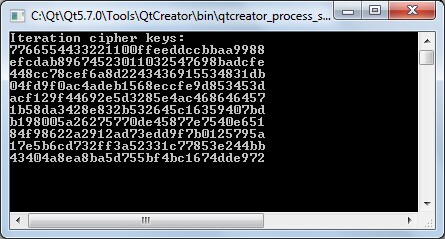
Зашифровываем
Как мы уже говорили, шифрование производится путем девяти итераций, включающих в себя преобразование X (сложение по модулю 2 исходного сообщения с очередным итерационным ключом), преобразование S и преобразование L, а также неполной десятой итерации, состоящей из преобразования X (сложение по модулю 2 с последним итерационным ключом):
void GOST_Kuz_Encript(const uint8_t *blk, uint8_t *out_blk)
{
int i;
memcpy(out_blk, blk, BLOCK_SIZE);
for(i = 0; i < 9; i++)
{
GOST_Kuz_X(iter_key[i], out_blk, out_blk);
GOST_Kuz_S(out_blk, out_blk);
GOST_Kuz_L(out_blk, out_blk);
}
GOST_Kuz_X(out_blk, iter_key[9], out_blk);
}
Перед запуском данной функции не забудь вызвать GOST_Kuz_Expand_Key, чтобы заполнить массив с итерационными ключами нужными значениями.
Расшифровываем
Расшифрование производится в обратном порядке и с использованием обратных преобразований:
void GOST_Kuz_Decript(const uint8_t *blk, uint8_t *out_blk)
{
int i;
memcpy(out_blk, blk, BLOCK_SIZE);
GOST_Kuz_X(out_blk, iter_key[9], out_blk);
for(i = 8; i >= 0; i--)
{
GOST_Kuz_reverse_L(out_blk, out_blk);
GOST_Kuz_reverse_S(out_blk, out_blk);
GOST_Kuz_X(iter_key[i], out_blk, out_blk);
}
}
Здесь также не стоит забывать про GOST_Kuz_Expand_Key, так как для расшифрования используются те же итерационные ключи, что и для зашифрования.

Заключение
Зашифровали блок, а что дальше? Если у нас сообщение больше, чем размер одного блока (128 бит)? О том, что делать дальше с зашифрованными блоками и как зашифровать какой-нибудь большой файл, говорится в другом стандарте — ГОСТ 34.13—2015. Данный ГОСТ предусматривает несколько режимов:
- режим простой замены;
- режим гаммирования;
- режим гаммирования с обратной связью по выходу;
- режим простой замены с зацеплением;
- режим гаммирования с обратной связью по шифртексту;
- режим выработки имитовставки.
Все это дело мы разберем позже, а если нужно срочно, то качай ГОСТ, изучай, разбирайся. Самое сложное (как зашифровать один 128-битный блок) мы уже выяснили. Дальше, как говорится, дело техники.