Погружение в ассемблер. Работаем с большими числами и делаем сложные математические вычисления

Простейшие операции над 32-битными числами

Сразу возникает вопрос: если регистры у нас 16-битные, то как с их помощью обрабатывать 32-битные числа? Ответ очевиден: мы просто будем задавать каждое число не одним регистром, а сразу двумя.

Только нам надо сначала определиться, какими регистрами и как мы будем для этого пользоваться. Давай не станем изобретать велосипед, а поищем подсказки в самом процессоре 8088.

У 8088 есть инструкция mul, которая умножает AX на 16-битный регистр и кладет результат в DX:AX. Также у него есть инструкция div, которая делит DX:AX на 16-битный регистр; результат попадает в регистр AX, а остаток — в DX. Еще у 8088 есть инструкция cwd. Она конвертирует знаковое 16-битное число из регистра AX в 32-битное число DX:AX.

Давай и мы, по примеру этих трех инструкций, тоже будем хранить 32-битные числа в DX:AX (в DX старшее слово, в AX — младшее). Но чтобы выполнять арифметические операции, нам нужно еще одно 32-битное число. Его, по аналогии с первым, будем хранить в CX:BX (в CX старшее слово, в BX — младшее).

Ну вот, мы с тобой условились, где и как хранить 32-битные числа. Теперь давай реализуем для них операцию сложения и операцию вычитания. Для этого нам пригодятся инструкции adc и sbb. Вот так выглядит сложение.

Удивлен, что операция сложения у нас заняла всего две инструкции? Сейчас объясню, что тут происходит. Дело в том, что, когда ты выполняешь инструкцию add, она не только складывает два числа, но и изменяет флаг переноса. Когда результат операции сложения не умещается в сдвоенный байт, инструкция add помещает старшую цифру результата (это всегда единица) во флаг переноса.

Инструкция adc dx, cx выполняет вот такую операцию: DX = DX + CX + перенос, то есть прибавляет к итоговому результату то значение, которое хранится во флаге переноса.

Теперь давай реализуем вычитание 32-битных чисел по такому же принципу.

Что тут происходит? Инструкция sub вычитает из одного числа другое, а еще изменяет флаг переноса. Когда операция вычитания делает «заем» из соседнего разряда, флаг переноса устанавливается в единицу.

Инструкция sbb dx, cx выполняет вот такую операцию: DX = DX – CX – перенос, то есть вычитает из итогового результата то значение, которое хранится во флаге переноса.

Мы с тобой успешно реализовали операции сложения и вычитания. Теперь давай реализуем логическое инвертирование и арифметическое инвертирование.

Чтобы сделать логическое инвертирование 32-битного числа (not), нам надо просто переключить все биты числа на противоположные.

Если требуется выполнить арифметическое инвертирование (neg), то есть поменять знак числа, нужно сделать то же самое, но только прибавить единицу к результату.

Реализуем операцию умножения двух 32-битных чисел

А теперь давай реализуем операцию умножения. Это уже будет посложнее. Здесь нужно вспомнить то, что ты изучал в начальной школе.

Ты же, надеюсь, еще не разучился умножать числа в столбик? На всякий случай напомню, что мы тут делаем.

Поочередно, справа налево, умножаем каждую цифру множимого на вторую цифру множителя. Так у нас получается первая строчка промежуточного результата. Затем умножаем каждую цифру множимого на первую цифру множителя. Так у нас получается вторая строчка промежуточного результата. Затем сдвигаем вторую строчку на один разряд влево и суммируем два промежуточных результата.

Получается, чтобы перемножить два двузначных числа, нам нужно выполнить четыре операции умножения. А если надо перемножить числа большей разрядности, то операций умножения потребуется еще больше.

Но это если «в роли цифры» у нас выступают цифры от 0 до 9. Однако, зная, что у процессора 8088 есть инструкция для умножения 16-битных чисел, мы для удобства можем в своем алгоритме умножения «назначить на роль цифры» сдвоенный байт. То есть будем считать значения вроде 0x6725 и 0x1561 не числами, а цифрами!

Почему это удобнее? Потому что для умножения двух 32-битных чисел (по две 16-битные цифры на каждое) нам понадобится всего четыре инструкции умножения. Тогда умножение двух 32-битных чисел можно будет реализовать вот так.

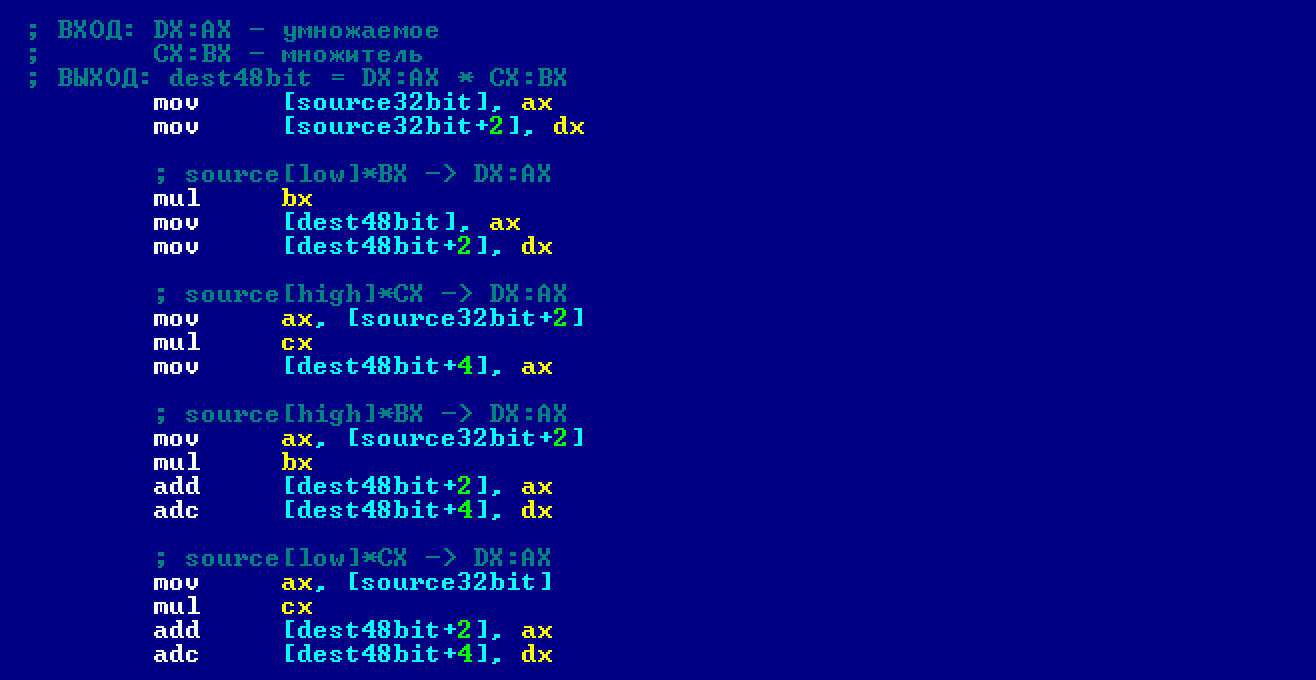
Умножение, конечно, выглядит сложновато по сравнению со сложением и вычитанием. Но не переживай, сейчас все объясню. Здесь весь алгоритм разделен на четыре операции умножения: по одной на каждое 16-битное слово. Точно так же, как на рисунке с умножением в столбик.

Кстати, если такой же алгоритм реализовывать на 32-битном процессоре, его можно расширить до операций над 64-битными числами, а если на 64-битном процессоре, то над 128-битными числами.

Но давай вернемся к нашему 16-битному алгоритму. Обрати внимание, здесь под результат отводится только 48 бит. А это значит, что если умножить, допустим, 0xFFFFFFFF на 0xFFFFFFFF, то старшие два байта потеряются. Чтобы они не терялись, нужно 64 бита, а не 48. Можешь в качестве домашнего задания доделать функцию — чтобы она возвращала 64-битный результат.

Продолжение доступно только участникам

Вариант 1. Присоединись к сообществу «Xakep.ru», чтобы читать все материалы на сайте

Членство в сообществе в течение указанного срока откроет тебе доступ ко ВСЕМ материалам «Хакера», позволит скачивать выпуски в PDF, отключит рекламу на сайте и увеличит личную накопительную скидку! Подробнее

-60% 1 год 9990 рублей 4000 р.

1 месяц 920 р.

Вариант 2. Открой один материал

Заинтересовала статья, но нет возможности стать членом клуба «Xakep.ru»? Тогда этот вариант для тебя! Обрати внимание: этот способ подходит только для статей, опубликованных более двух месяцев назад.

Я уже участник «Xakep.ru»