В прошлый раз (в ноябре 2014-го; мне очень стыдно, что я так затянул с продолжением!) я рассказывал о базовых возможностях языка R. Несмотря на наличие всех привычных управляющих конструкций, таких как циклы и условные блоки, классический подход к обработке данных на основе итерации далеко не лучшее решение, поскольку циклы в R необыкновенно медлительны. Поэтому сейчас я расскажу, как на самом деле нужно работать с данными, чтобы процесс вычислений не заставлял тебя выпивать слишком много чашек кофе в ожидании результата. Кроме того, некоторое время я посвящу рассказу о том, как пользоваться современными средствами визуализации данных в R. Потому что удобство представления результатов обработки данных на практике не менее важно, чем сами результаты. Начнем с простого.
Векторные операции
Как мы помним, базовым типом в R является вовсе не число, а вектор, и основные арифметические операции действуют на векторы поэлементно:
> x <- 1:6; y <- 11:17
> x + y
[1] 12 14 16 18 20 22 18
> x > 2
[1] FALSE FALSE TRUE TRUE TRUE TRUE
> x * y
[1] 11 24 39 56 75 96 17
> x / y
[1] 0.09090909 0.16666667 0.23076923 0.28571429 0.33333333 0.37500000
[7] 0.05882353Тут все довольно просто, однако вполне логично задаться вопросом: что же будет, если длина векторов не совпадет? Если мы, скажем, напишем k <- 2, то будет ли x * k соответствовать умножению вектора на число в математическом смысле? Короткий ответ — да. В более общем случае, когда длина векторов не совпадает, меньший вектор просто продолжается повторением:
> z <- c(1, 0.5)
> x * z
[1] 1 1 3 2 5 3Примерно так же обстоят дела и с матрицами.
> x <- matrix(1:4, 2, 2); y <- matrix(rep(2,4), 2, 2)
> x * y
[,1] [,2]
[1,] 2 6
[2,] 4 8
> x / y
[,1] [,2]
[1,] 0.5 1.5
[2,] 1.0 2.0При этом «нормальное», а не поразрядное умножение матриц будет выглядеть так:
> x %*% y
[,1] [,2]
[1,] 8 8
[2,] 12 12Все это, конечно, очень хорошо, однако что же делать, когда нам нужно применять свои собственные функции к элементам векторов или матриц, то есть как это можно сделать без цикла? Подход, который используется в R для решения данной проблемы, очень схож с тем, к чему мы привыкли в функциональных языках, — все это напоминает функцию map в Python или Haskell.
Полезная функция lapply и ее друзья
Первая функция в этом семействе — это lapply. Она позволяет применять заданную функцию к каждому элементу списка или вектора. Причем результатом будет именно список независимо от типа аргумента. Простейший пример с применением лямбда-функций:
> q <- lapply(c(1,2,4), function(x) x^2)
> q
[[1]]
[1] 1
[[2]]
[1] 4
[[3]]
[1] 16Если функция, которую нужно применить к списку или вектору, требует более одного аргумента, то эти аргументы можно передать через lapply.
> q <- lapply(c(1,2,4), function(x, y) x^2 + y, 3)Со списком функция работает аналогичным образом:
> x <- list(a=rnorm(10), b=1:10)
> lapply(x, mean)Здесь функция rnorm задает нормальное распределение (в данном случае десять нормально распределенных чисел в диапазоне от 0 до 1), а mean вычисляет среднее значение. Функция sapply полностью аналогична функции lapply за исключением того, что она пытается упростить результат. К примеру, если каждый элемент списка длины 1, то вместо списка вернется вектор:
> sapply(c(1,2,4), function(x) x^2)
[1] 1 4 16Если результатом будет список из векторов одинаковой длины, то функция вернет матрицу, если же ничего не понятно, то просто список, как lapply.
> x <- list(1:4, 5:8)
> sapply(x, function(x) x^2)
[,1] [,2]
[1,] 1 25
[2,] 4 36
[3,] 9 49
[4,] 16 64Для работы с матрицами удобно использовать функцию apply:
> x <- matrix(rnorm(50), 5, 10)
> apply(x, 2, mean)
> apply(x, 1, sum)Здесь для начала мы создаем матрицу из пяти строк и десяти столбцов, потом сначала считаем среднее по столбцам, а затем сумму в строках. Для полноты картины следует отметить, что задачи вычисления среднего и суммы по строкам настолько часто встречаются, что в R для этого предусмотрены специальные функции rowSums, rowMeans, colSums и colMeans.
Также функцию apply можно применять для многомерных массивов:
> arr <- array(rnorm(2 * 2 * 10), c(2, 2, 10))
> apply(arr, c(1,2), mean)Последний вызов можно заменить на более удобный для чтения вариант:
> rowMeans(arr, dim = 2)Перейдем к функции mapply, представляющей собой многомерный аналог lapply. Начнем с простого примера, который можно найти прямо в стандартной документации к R:
> mapply(rep, 1:4, 4:1)
[[1]]
[1] 1 1 1 1
[[2]]
[1] 2 2 2
[[3]]
[1] 3 3
[[4]]
[1] 4Как можно видеть, здесь происходит применение функции rep к набору параметров, которые генерируются из двух последовательностей. Сама функция rep просто повторяет первый аргумент то число раз, которое указано в качестве второго аргумента. Таким образом, предыдущий код просто эквивалентен следующему:
> list(rep(1,4), rep(2,3), rep(3,2), rep(4,1))Иногда бывает необходимо применить функцию к какой-то части массива. Это можно сделать с помощью функции tapply. Давай рассмотрим следующий пример:
> x <- c(rnorm(10, 1), runif(10), rnorm(10,2))
> f <- gl(3,10)
> tapply(x,f,mean)Сначала мы создаем вектор, части которого формируются из случайных величин с различным распределением, далее мы генерируем вектор из факторов, который представляет собой не что иное, как десять единиц, потом десять двоек и столько же троек. Затем вычисляем среднее по соответствующим группам. Функция tapply по умолчанию пытается упростить результат. Эту опцию можно выключить, указав в качестве параметра simplify=FALSE.
> tapply(x, f, range, simplify=FALSE)Когда говорят о функциях apply, обычно также говорят о функции split, которая разбивает вектор на части, аналогично tapply. Так, если мы вызовем split(x, f) то получим список из трех векторов. Таким образом, пара lapply/split работает так же, как и tapply со значением simplify, равным FALSE:
> lapply(split(x, f), mean)Функция split полезна и за пределами работы с векторами: ее также можно использовать и для работы с фреймами данных. Рассмотрим следующий пример (я позаимствовал его из курса R Programming на Coursera):
> library(datasets)
> head(airquality)
Ozone Solar.R Wind Temp Month Day
1 41 190 7.4 67 5 1
2 36 118 8.0 72 5 2
3 12 149 12.6 74 5 3
4 18 313 11.5 62 5 4
5 NA NA 14.3 56 5 5
6 28 NA 14.9 66 5 6
> s <- split(airquality, airquality$Month)
> lapply(s, function(x) colMeans(x[, c("Ozone", "Solar.R", "Wind")]))Здесь мы работаем с набором данных, который содержит информацию о состоянии воздуха (содержание озона, солнечная радиация, ветер, температура в градусах Фаренгейта, месяц и день). Мы можем легко сделать отчет о среднемесячных показателях, используя split и lapply, как показано в коде. Использование sapply, однако, даст нам результат в более удобном виде:
> sapply(s, function(x) colMeans(x[, c("Ozone", "Solar.R", "Wind")]))
5 6 7 8 9
Ozone NA NA NA NA NA
Solar.R NA 190.16667 216.483871 NA 167.4333
Wind 11.62258 10.26667 8.941935 8.793548 10.1800Как видно, некоторые значения величин не определены (и для этого используется зарезервированное значение NA). Это означает, что какие-то (хотя бы одно) значения в колонках Ozone и Solar.R были также не определены. В этом смысле функция colMeans ведет себя совершенно корректно: если есть какие-то неопределенные значения, то и среднее, таким образом, не определено. Проблему можно решить, принудив функцию не учитывать значения NA с помощью параметра na.rm=TRUE:
> sapply(s, function(x) colMeans(x[, c("Ozone", "Solar.R", "Wind")], na.rm=TRUE))
5 6 7 8 9
Ozone 23.61538 29.44444 59.115385 59.961538 31.44828
Solar.R 181.29630 190.16667 216.483871 171.857143 167.43333
Wind 11.62258 10.26667 8.941935 8.793548 10.18000Зачем нужно такое количество функций для решения очень схожих между собой задач? Думаю, такой вопрос задаст каждый второй человек, который все это прочитал. Все эти функции на самом деле пытаются решить проблему обработки векторных данных без использования циклов. Но одно дело — добиться высокой скорости обработки данных и совершенно другое — получить хотя бы часть той гибкости и контроля, которую обеспечивают такие управляющие конструкции, как циклы и условные операторы.
Визуализация данных
Система R необыкновенно богата на средства визуализации данных. И тут передо мной стоит непростой выбор — о чем вообще говорить, если область так велика. Если в случае программирования есть какой-то базовый набор функций, без которого ничего не сделать, то в визуализации огромное количество различных задач и каждая из них (как правило) может быть решена несколькими способами, каждый из которых имеет свои плюсы и минусы. Более того, всегда есть множество опций и пакетов, позволяющих решать эти задачи различным образом.
Про стандартные средства визуализации в R написано очень много, поэтому здесь мне бы хотелось рассказать о чем-то более интересном. В последние годы все более популярным становится пакет ggplot2, вот про него и поговорим.
Для того чтобы начать работать с ggplot2, нужно установить библиотеку с помощью команды install.package("ggplot2"). Далее подключаем ее для использования:
> library("ggplot2")
> head(diamonds)
carat cut color clarity depth table price x y z
1 0.23 Ideal E SI2 61.5 55 326 3.95 3.98 2.43
2 0.21 Premium E SI1 59.8 61 326 3.89 3.84 2.31
3 0.23 Good E VS1 56.9 65 327 4.05 4.07 2.31
4 0.29 Premium I VS2 62.4 58 334 4.20 4.23 2.63
5 0.31 Good J SI2 63.3 58 335 4.34 4.35 2.75
6 0.24 Very Good J VVS2 62.8 57 336 3.94 3.96 2.48
> head(mtcars)
mpg cyl disp hp drat wt qsec vs am gear carb
Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
Valiant 18.1 6 225 105 2.76 3.460 20.22 1 0 3 1Данные diamonds и mtcars являются частью пакета ggplot2, и именно с ними мы будем сейчас работать. С первым все понятно — это данные о бриллиантах (чистота, цвет, стоимость и прочее), а второй сет — это данные дорожных тестов (количество миль на галлон, количество цилиндров...) автомобилей 1973–1974 годов выпуска из американского журнала Motor Trends. Более подробную информацию о данных (к примеру, размерность) можно получить, набрав ?diamonds или ?mtcars.
Для визуализации в пакете предусмотрено много функций, из которых для нас сейчас будет наиболее важна qplot. Функция ggplot предоставляет существенно больше контроля над процессом. Все, что можно сделать с помощью qplot, также можно сделать и с помощью ggplot. Рассмотрим это на простом примере:
> qplot(clarity, data=diamonds, fill=cut, geom="bar")Того же самого эффекта можно достичь и функцией ggplot:
> ggplot(diamonds, aes(clarity, fill=cut)) + geom_bar()Однако вызов qplot выглядит проще. На рис. 1 можно увидеть, как строится зависимость количества бриллиантов с различным качеством огранки (cut) от чистоты (clarity).
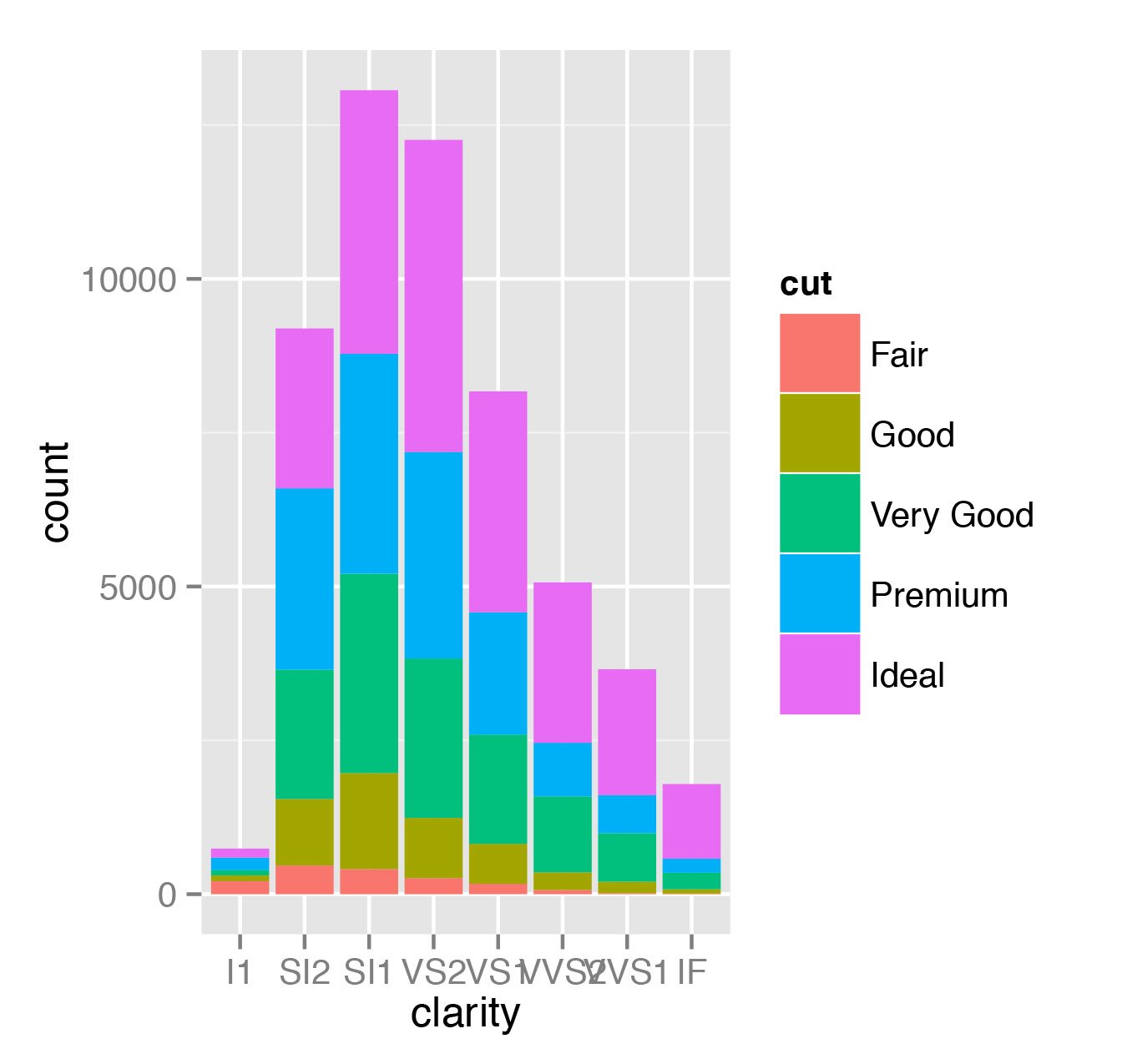
Теперь построим зависимость пробега на единицу топлива автомобилей от их массы. Полученная точечная диаграмма (или диаграмма рассеивания scatter plot) представлена
на рис. 2.
> qplot(wt, mpg, data=mtcars)Можно также еще добавить цветовое отображение показателя времени разгона на четверть мили (qsec):
> qplot(wt, mpg, data=mtcars, color=qsec)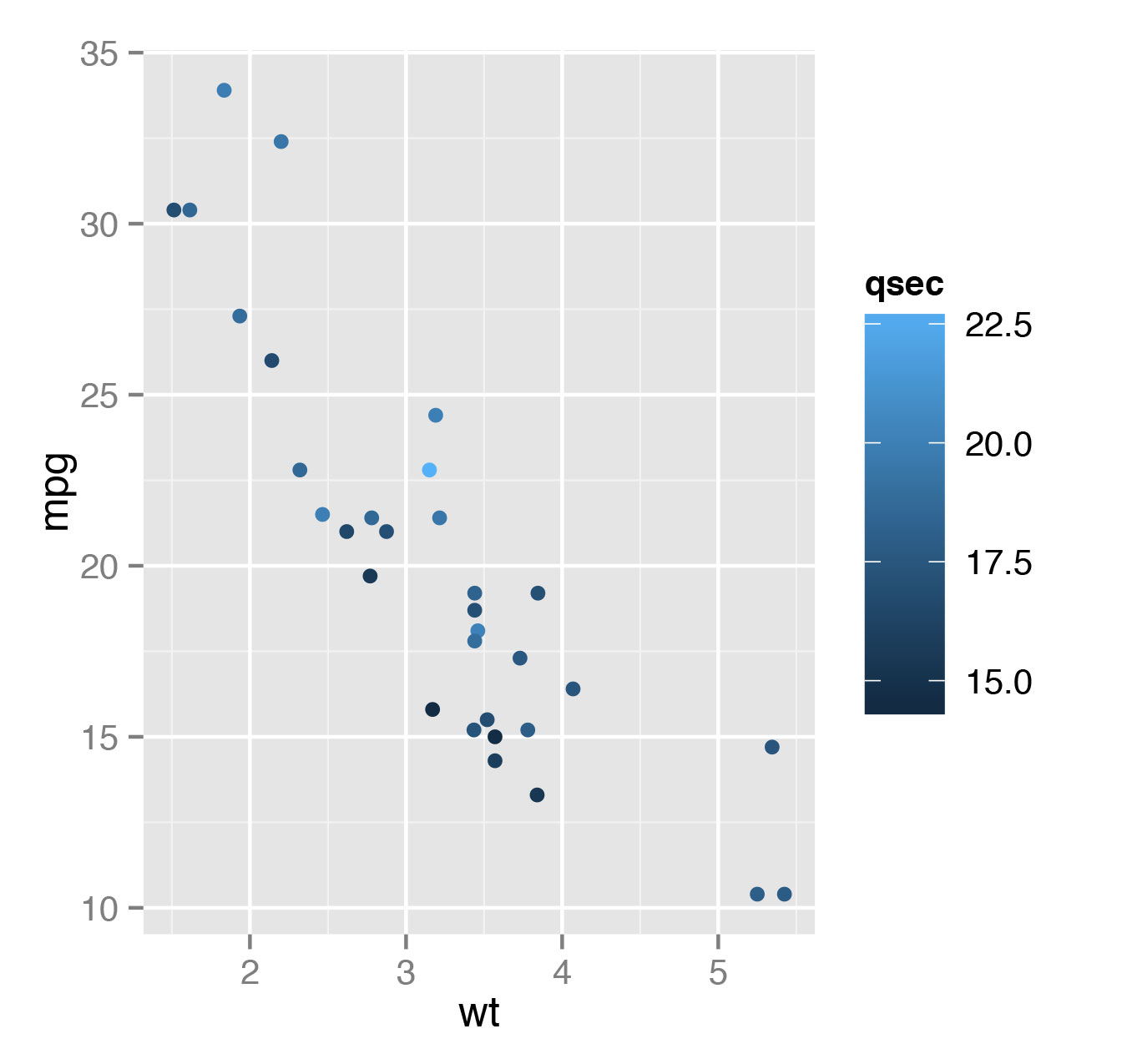
При визуализации также можно преобразовывать данные:
> qplot(log(wt), mpg - 10, data=mtcars)В некоторых случаях дискретное цветовое деление выглядит более репрезентативно, нежели непрерывное. К примеру, если мы хотим отобразить цветом информацию о количестве цилиндров вместо времени разгона, то нужно указать, что величина носит дискретный характер (рис. 3):
> qplot(wt, mpg, data=mtcars, color=factor(cyl))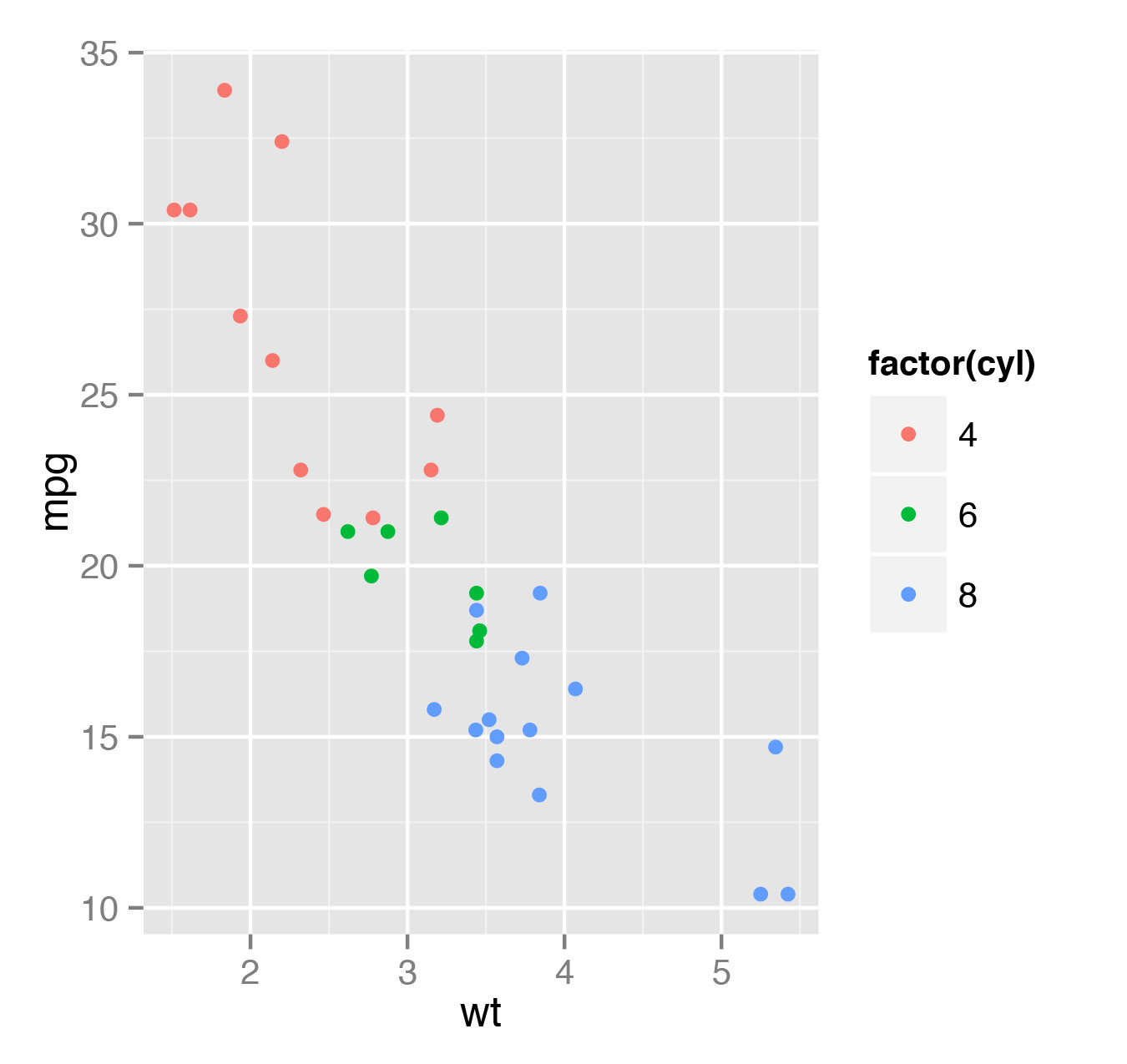
Также можно менять размер точек, используя, к примеру, size=3. Если ты собираешься печатать графики на черно-белом принтере, то лучше не использовать цвета, а вместо этого менять форму маркера в зависимости от фактора. Это можно сделать, заменив color=factor(cyl) на shape=factor(cyl).
Тип графика задается с помощь параметра geom, и в случае точечных диаграмм значение этого параметра равно "points".
Теперь пускай мы хотим просто построить гистограмму по количеству автомобилей с соответствующим значением цилиндров:
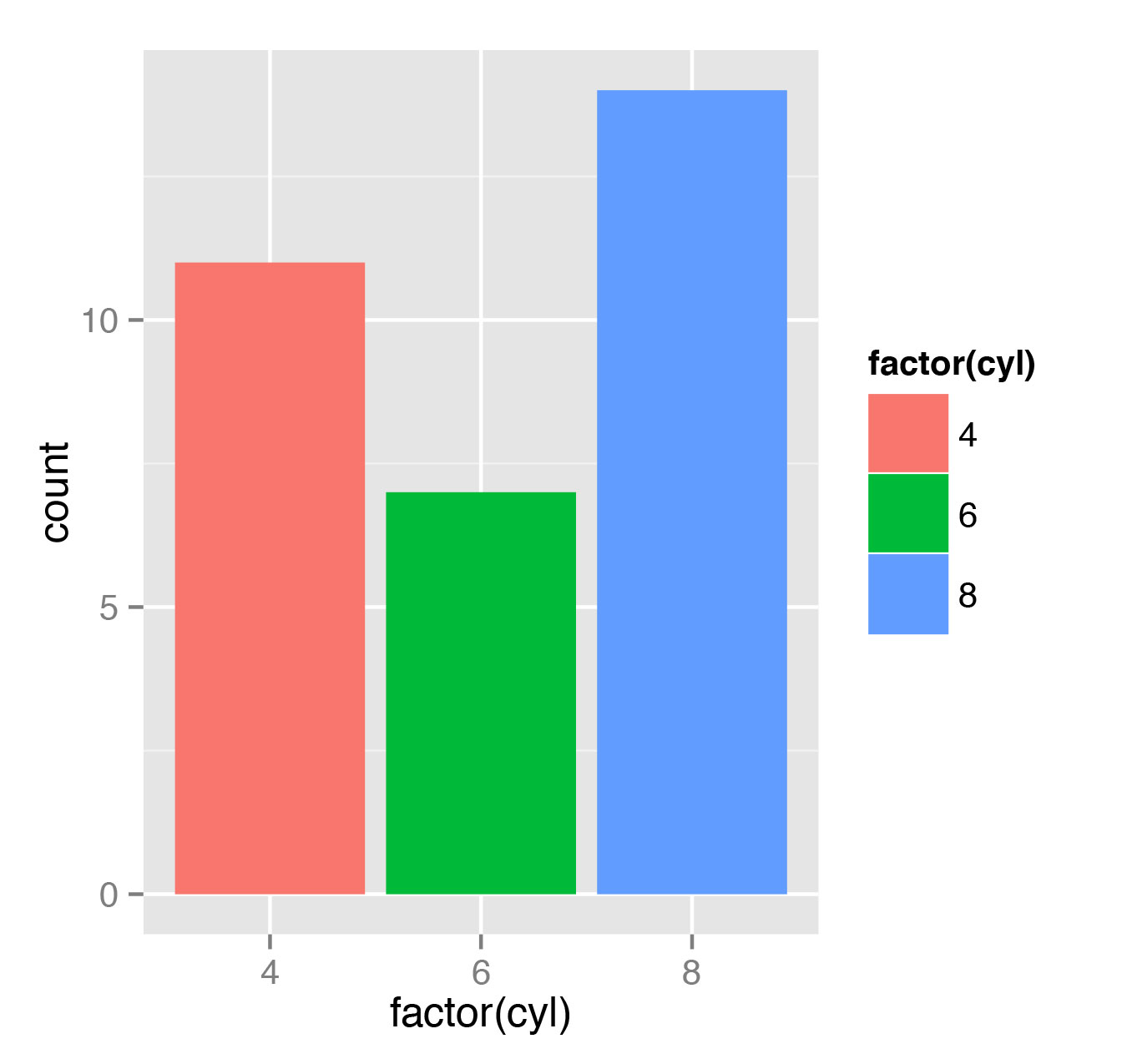
> qplot(factor(cyl), data=mtcars, geom="bar")
> qplot(factor(cyl), data=mtcars, geom="bar", color=factor(cyl))
> qplot(factor(cyl), data=mtcars, geom="bar", fill=factor(cyl))Первый вызов просто рисует три гистограммы для различных значений цилиндров. Надо сказать, что первая попытка придать цвет гистограмме не приведет к ожидаемому результату — черные столбики так и будут черными, только получат цветной контур. А вот последний вызов qplot сделает красивую гистограмму, как показано на рис. 4.
Тут следует внести ясность. Дело в том, что текущий построенный нами объект не является гистограммой в строгом смысле слова. Обычно под гистограммой понимают аналогичное отображение для непрерывных данных. В английском языке bar chart (это то, что мы только что сделали) и histogram — это два различных понятия (см. соответствующие статьи в Википедии). Здесь я, с некоторой тяжестью на душе, буду использовать слово «гистограмма» для обоих понятий, полагая, что сама природа данных говорит за себя.
Если вернуться к рис. 1, то ggplot2 предоставляет несколько полезных опций в позиционирование графиков (по умолчанию используется значение position="stack"):
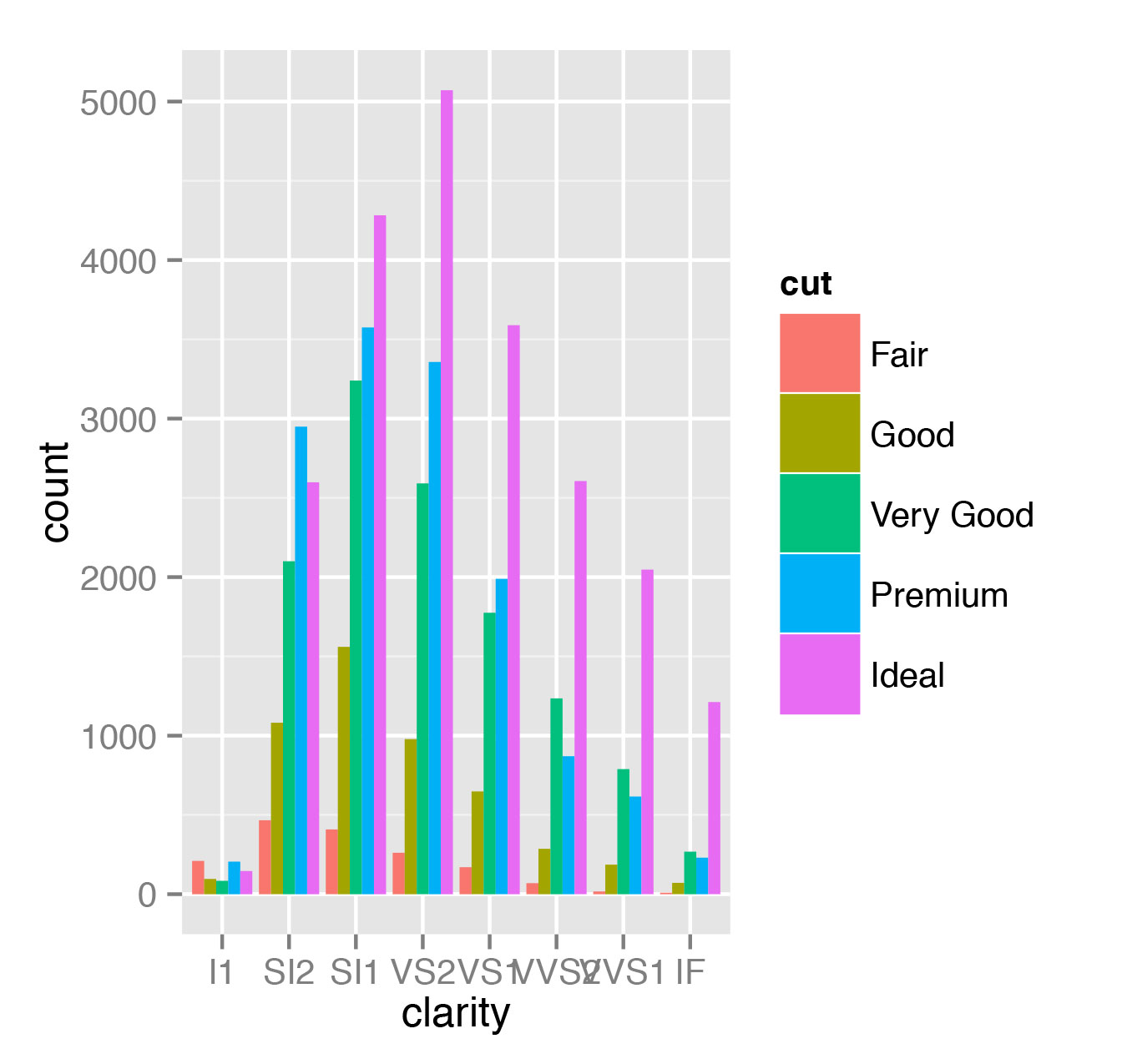
> qplot(clarity, data=diamonds, geom="bar", fill=cut, position="dodge")
> qplot(clarity, data=diamonds, geom="bar", fill=cut, position="fill")
> qplot(clarity, data=diamonds, geom="bar", fill=cut, position="identity")Первый из предложенных вариантов строит диаграммы рядом, как показано на рис. 5, второй показывает доли бриллиантов различного качества огранки в общем числе бриллиантов заданной чистоты (рис. 6).
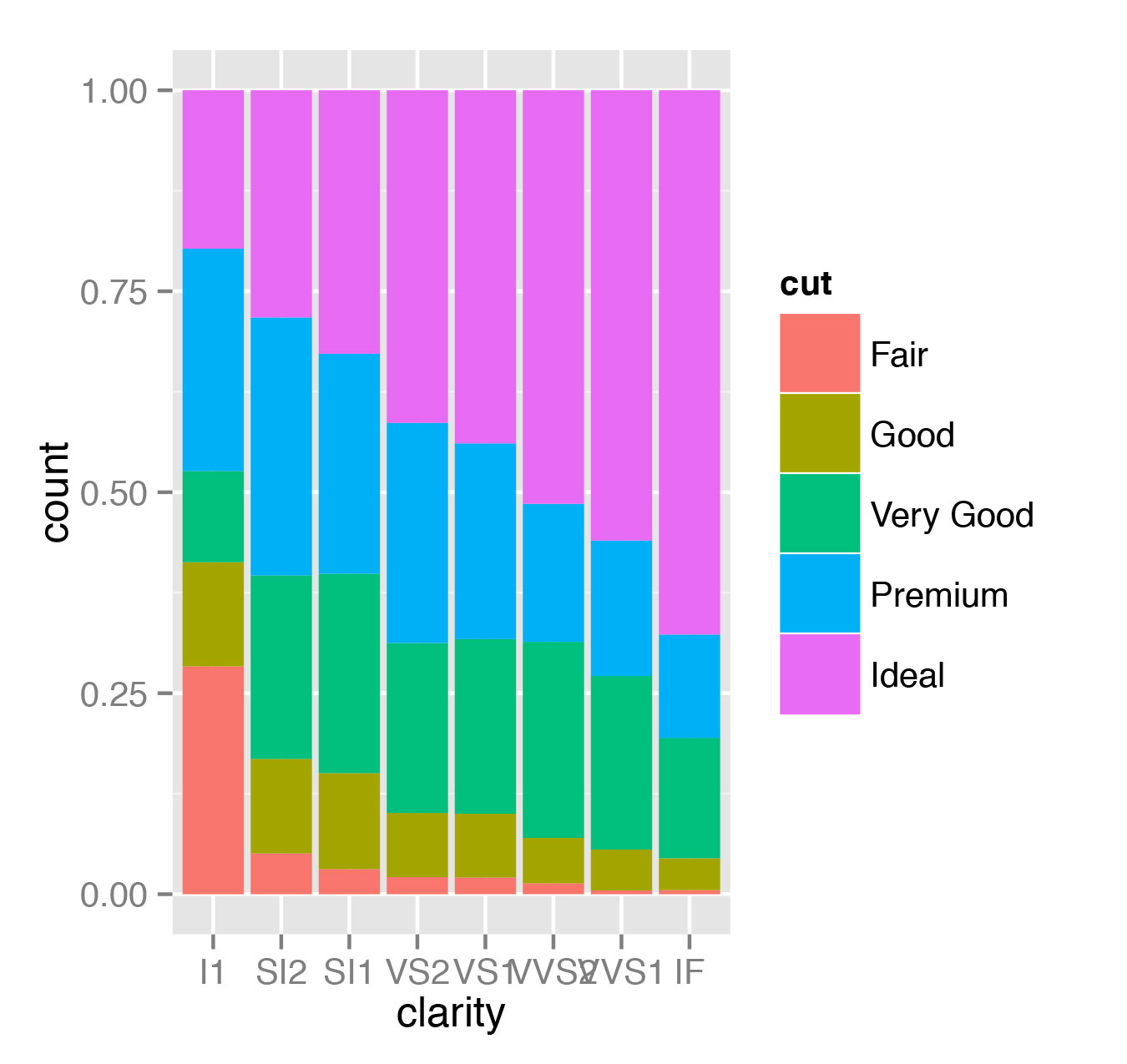
Теперь рассмотрим пример настоящей гистограммы:
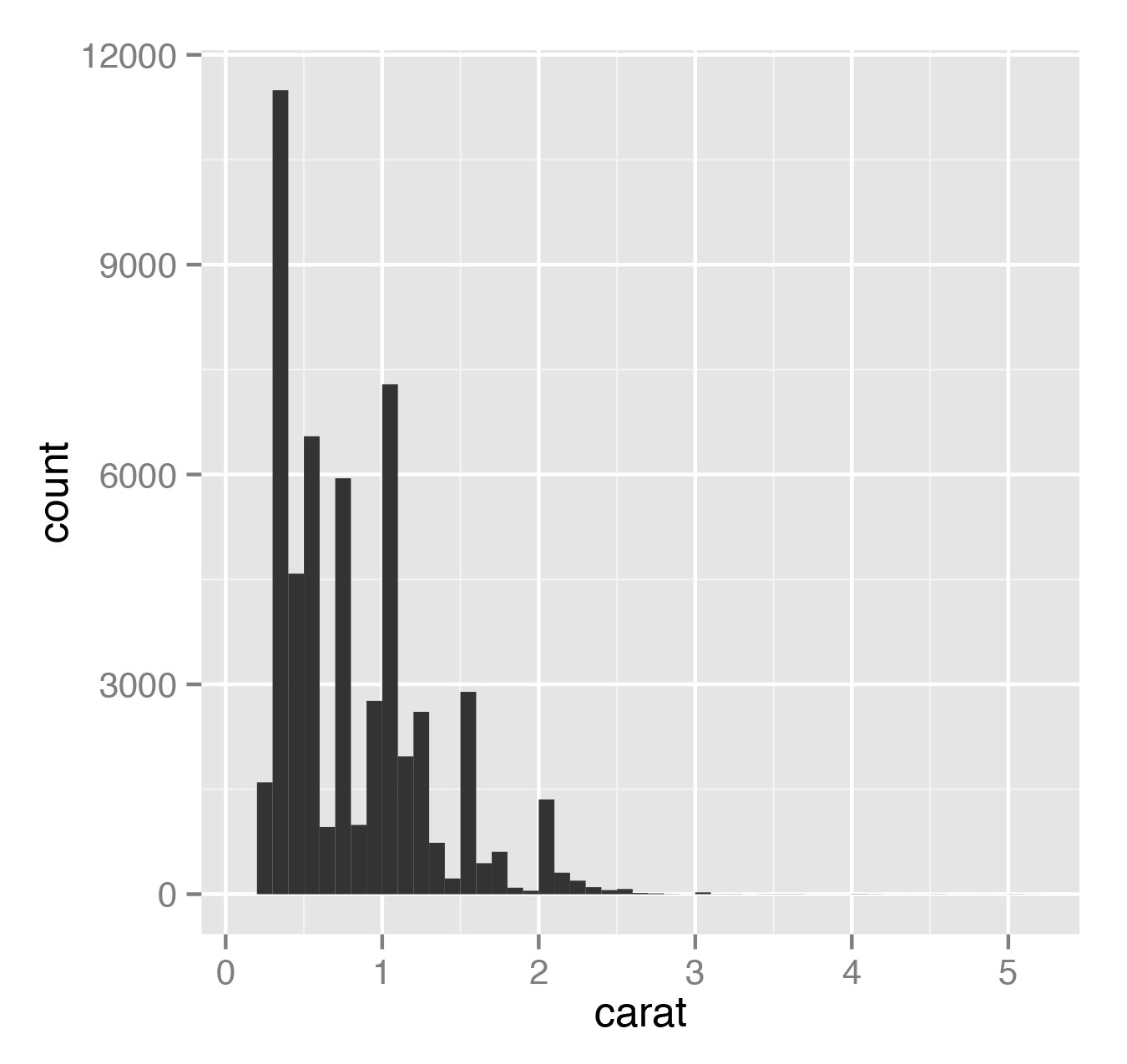
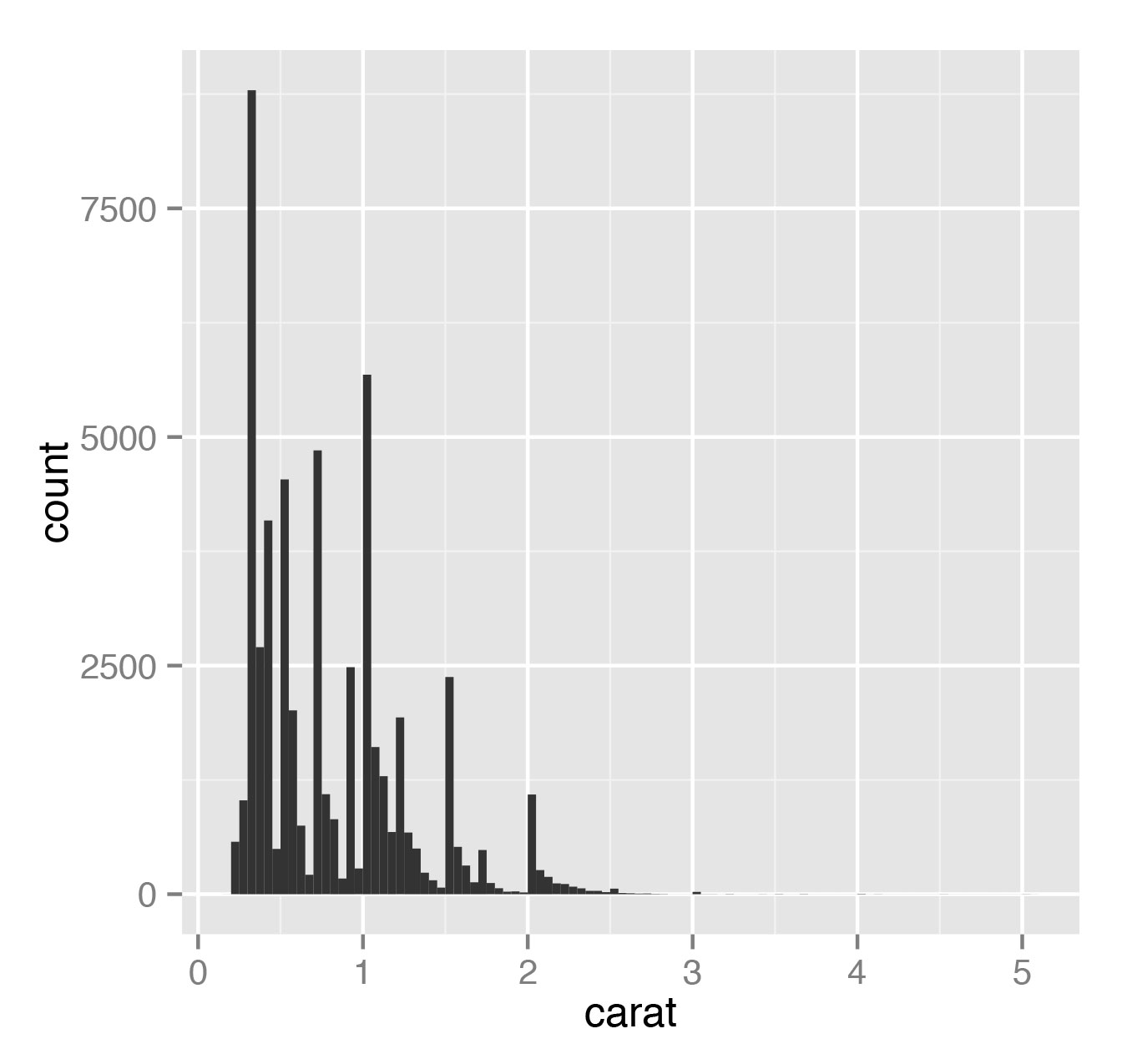
> qplot(carat, data=diamonds, geom="histogram", bandwidth=0.1)
> qplot(carat, data=diamonds, geom="histogram", bandwidth=0.05)Здесь параметр bandwidth как раз показывает, какой ширины полоса в гистограмме. Гистограмма показывает, сколько данных приходится на какой диапазон. Результаты представлены на рис. 7 и 8.
Иногда, когда нам нужно построить модель (линейную или, скажем, полиномиальную), мы можем сделать это прямо в qplot и увидеть результат. К примеру, мы можем построить график зависимости mpg от массы wt прямо поверх точечной диаграммы:
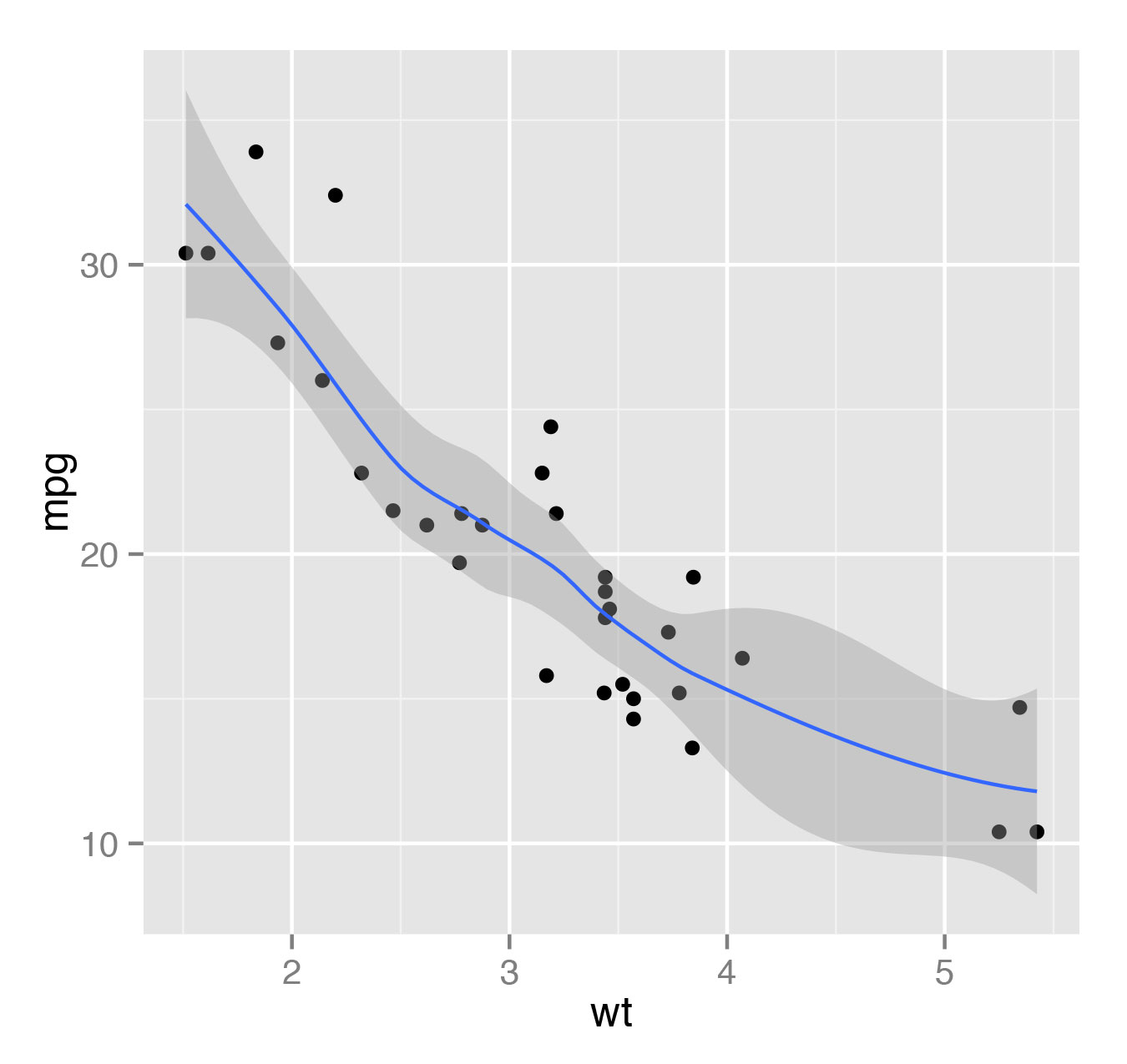
> qplot(wt, mpg, data=mtcars, geom=c("point", "smooth"))По умолчанию в качестве модели будет использоваться локальная полиномиальная регрессия (method="loess"). Результат работы будет выглядеть, как показано на рис. 9, где темно-серая полоса — это стандартная ошибка. Она отображается по умолчанию, ее отображение можно выключить, написав se=FALSE.
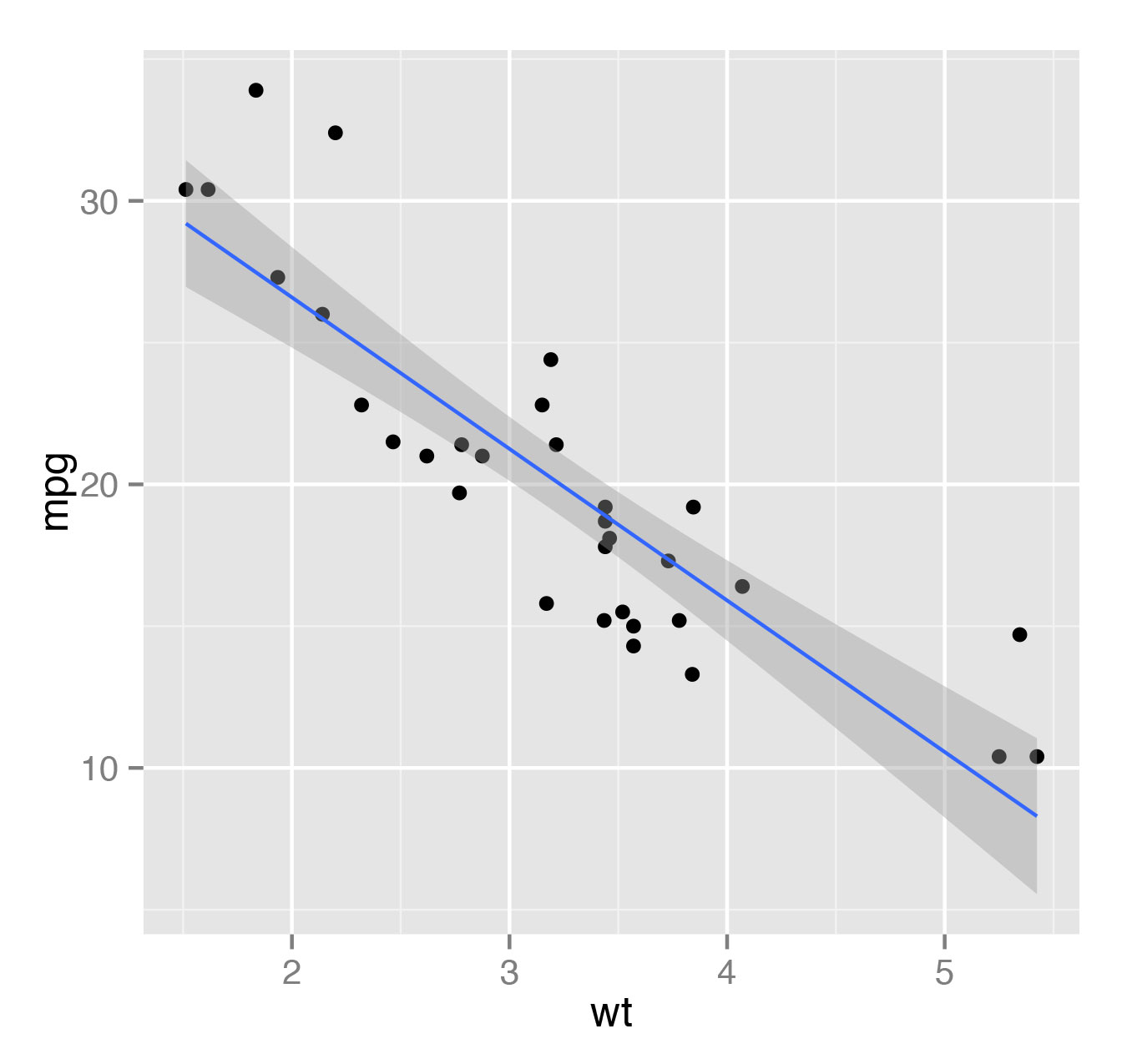
Если же мы хотим попробовать натянуть линейную модель на эти данные, то это можно сделать, просто указав method=lm (рис. 10).
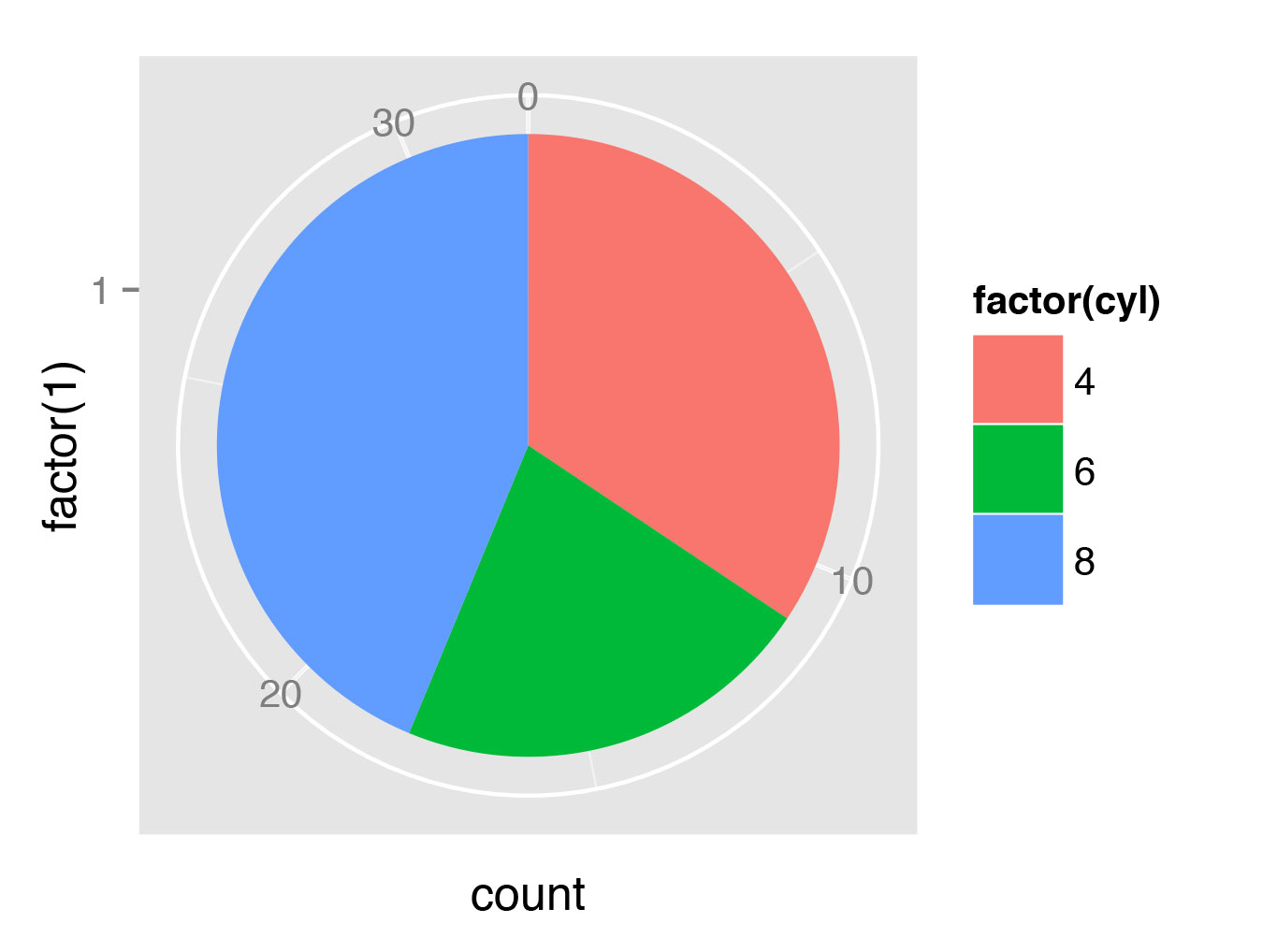
И напоследок, конечно же, нужно показать, как строить круговые диаграммы:
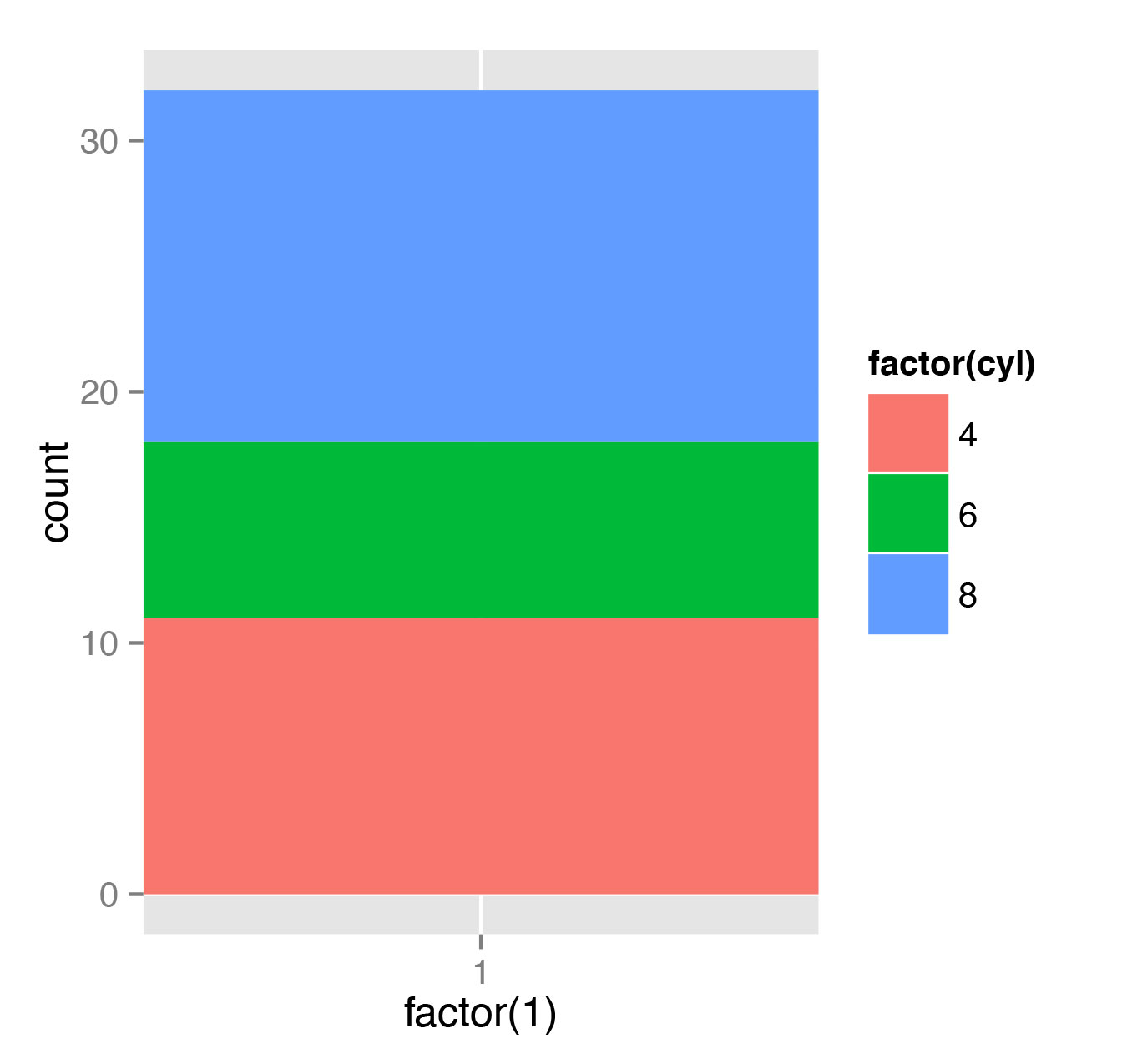
> t <- ggplot(mtcars, aes(x=factor(1), fill=factor(cyl))) + geom_bar(width=1)
> t + coord_polar(theta="y")Здесь мы воспользуемся более гибкой функцией ggplot. Это работает так: сначала мы строим график, отображающий доли автомобилей с разным количеством цилиндров в общей массе (рис. 11), затем переводим график в полярные координаты (рис. 12).
Вместо заключения
Вот мы и освоились с использованием R. Что дальше? Понятно, что здесь даны самые базовые возможности ggplot2 и рассмотрены вопросы, связанные с векторизацией. Есть несколько хороших книг по R, которые стоит упомянуть, и к ним, вне всякого сомнения, стоит обращаться чаще, чем к услугам корпорации очень навязчивого добра. Во-первых, это книга Нормана Матлоффа (Norman Matloff) The Art of R Programming. Если же у тебя уже есть опыт в программировании на R, то тебе пригодится The R Inferno, написанная П. Бернсом (Patrick Burns). Классическая книга Software for Data Analysis Джона Чамберса (John Chambers) также вполне уместна.
Если говорить о визуализации в R, то есть хорошая книга R Graphics Cookbook В. Чанга (Winston Chang). Примеры для ggplot2 в этой статье были взяты из Tutorial: ggplot2. До встречи в следующей статье «Анализ данных и машинное обучение в R»!