Содержание статьи
Знания и умения, которые раньше требовались только в небольшом количестве областей, таких как финансовый сектор и вычислительная физика, сейчас могут быть применены практически всюду.
Чем больше данных создается (намеренно или как побочный продукт реализации других процессов), тем больше специалистов в этой области востребовано. Многие думают, что работа с данными доступна только профессиональным математикам. Здесь можно провести аналогию с программированием: изначально оно было сферой деятельности математиков, но с развитием инструментов получило широкое распространение. Похожие изменения происходят сейчас и в области анализа данных. Перед тобой первая статья из серии материалов, в которых я расскажу о методах и инструментах, применяющихся для анализа и обработки (в том числе и больших) данных.
Работа мечты и buzzwords
Когда я учился на кафедре вычислительной физики СПбГУ, мне говорили, что из физиков получаются отличные системные администраторы. Не самое мотивирующее высказывание, которое можно услышать... И надо сказать, численные методы и статистика могут отвратить от себя почти любого человека. Именно поэтому во время обучения меня гораздо больше интересовало программирование. Если бы кто‑то тогда сказал мне, что я буду применять знания из области численных методов в своей деятельности и создам компанию, которая будет заниматься исследованиями в области обработки данных, то я бы ему просто не поверил. Однако все случилось именно так.
В последнее время одним из самых часто звучащих трендов в бизнесе является работа с большими данными (big data) и применение анализа данных (data mining) для достижения определенных целей компании. Цели эти, как правило, сводятся к извлечению коммерческой выгоды, хотя бывают и исключения: Google, например, смог предсказать развитие эпидемии гриппа на основе запросов пользователей с учетом географической привязки и путем сопоставления с информацией о предыдущих эпидемиях.
Выручка компании Amazon возросла на 20% после того, как на сайте внедрили систему, позволяющую адаптировать интерфейс и содержимое страниц индивидуально под каждого пользователя на основании истории его покупок и данных о том, какие товары чаще всего приобретаются вместе.
Существуют и более экзотические примеры применения анализа данных в коммерции. Еще в 2004 году сеть супермаркетов Wal-Mart готовилась к наступлению урагана «Фрэнсис» и проанализировала то, как меняется спрос на товары непосредственно перед бедствием. И хотя такие полученные результаты, как приобретение большего количества воды в бутылках, было легко спрогнозировать, другие выявленные закономерности оказались не вполне очевидными: после обработки огромного количества данных оказалось, что спрос на земляничное печенье перед ураганом возрастает в семь раз по сравнению с нормальным уровнем спроса, а первое место среди товаров повышенного спроса занимает пиво.
Многие компании на сегодняшний день уже располагают существенным количеством данных или начинают их собирать, рассчитывая использовать их для повышения эффективности работы. В связи с этим спрос на специалистов в области неуклонно растет.
По данным консалтинговой компании McKinsey, к 2018 году только в США недостаток специалистов в области анализа данных будет составлять от 140 до 190 тысяч, а дефицит менеджеров, понимающих, как использовать большие данные для принятия решений, в десять раз больше.
Последнее утверждение может показаться необоснованным, однако, если подумать, в этом есть смысл: если менеджеры не будут понимать, зачем нужны большие данные и какая от этого польза, то даже наличие очень талантливого аналитика в штате ничего не решит.
Анализ данных и его применение
При анализе данных почти каждая задача уникальна. Однако уникальность рассматриваемого случая не означает, что для его решения необходимо изобретать новый метод. Как правило, каждая задача может быть представлена как декомпозиция уже хорошо известных задач.
В этом разделе мы рассмотрим задачи, встречающиеся при работе с данными наиболее часто. Обычно выделяют следующие типы:
- классификация;
- регрессия;
- поиск подобия;
- кластеризация;
- группировка в соответствии с совместным появлением;
- определение профиля;
- предсказания связи;
- редукция данных;
- моделирование причинно‑следственных связей.
Под классификацией понимают задачу определения того, попадет ли конкретный объект в один из классов (точно или с некоторой вероятностью). Классы, как правило, предполагаются непересекающимися. Примером такой задачи может служить проверка сообщения в электронной почте или социальной сети на предмет спама.
Регрессия — это также одна из самых часто встречающихся задач, в которой требуется оценить значение целевого параметра в зависимости от значений исходных параметров. Положим, что у нас есть набор значений среднего балла в школе и в университете для некоторого количества учеников. Но наш набор дискретный, то есть не покрывает все множество возможных оценок. Если ты хочешь предсказать значение среднего балла в университете, то нужно как раз решить задачу регрессии, то есть отыскать модель, которая позволяла бы на основании известных данных находить предполагаемое значение любого ученика.
Эти две задачи принадлежат к классу задач машинного обучения с учителем. В таких задачах мы имеем размеченное заранее множество (когда для каждого набора признаков дано значение искомого параметра, например принадлежность к классу спам / не спам или значение среднего балла в университете), на основе которого строится модель. По сути, обе задачи занимаются предсказанием, только в случае классификации значение дискретно (если речь не идет о 100% вероятности попадания в класс), а в случае регрессии непрерывно.
Задача поиска подобия — это попытка идентифицировать похожие объекты на основе данных, относящихся к ним. Типичным примером такой задачи служит задача предоставления рекомендаций пользователю на основании его предыдущих покупок и предпочтений.
Кластеризация позволяет группировать объекты согласно их подобию, однако без какой‑либо четко зафиксированной цели, например, если мы хотим выяснить, образуют ли наши покупатели естественные группы согласно заданному набору признаков. Очевидные кластеры, сформированные на основе какого‑то одного признака, не так интересны. Так, разделить покупателей или пользователей по половому признаку довольно тривиально. Однако обычно интересны группы, которые связаны с сегментацией рынка. К примеру, это могут быть кластеры из пользователей в определенной возрастной группе и с определенным семейным положением. Более того, кластеры могут существенно различаться в рамках одного набора данных в зависимости от выбора признаков.
Группировка в соответствии с совместным появлением может быть хорошо проиллюстрирована на известном примере с интернет‑магазином и вопросом «Какие товары обычно покупают вместе?». На основе таких данных также можно успешно строить систему рекомендаций. В отличие от задачи поиска подобия, где требуется найти похожие товары вне зависимости от поведения пользователя, здесь именно поведение пользователя определяет способ группировки.
Часто бывает необходимо определить поведенческий портрет пользователя, чтобы оптимизировать продажи или работу с клиентами. В контексте информационной безопасности это также используется для выявления аномалий и мошенничества.
С появлением социальных сетей новый толчок получила отдельная область анализа данных, которая так и называется — анализ социальных сетей, или SNA. Данная область разрабатывалась еще социологами задолго до появления Facebook, но в наше время получила совершенно новое предназначение. В данной области часто встречается задача, известная как предсказание связи, когда на основании данных об общих друзьях двух конкретных людей можно сказать, являются ли эти двое друзьями или нет. Особенности социального графа или графа в какой‑либо похожей задаче позволяют оценивать такой показатель, как сила связи.
Надо сказать, что эта задача также встречается и вне социальных сетей как часть системы рекомендаций.
Предобработка данных вообще представляет собой отдельную область, но здесь мы ограничимся обсуждением только одной задачи. Когда речь заходит о больших объемах данных, размер задачи становится существенным, и поэтому во многих случаях приходится иметь дело с задачей редукции данных, то есть уменьшением количества данных, используемых в процессе анализа. Однако стоит иметь в виду, что уменьшение множества может привести к потере значимых данных. И в этом смысле задача редукции — это прежде всего поиск компромиссов между сокращением объема данных и сохранением значимой информации.
И последняя задача, о которой нужно сказать, — это моделирование причинноследственных связей.
Моделирование помогает установить влияние одних действий или событий на другие. Такой вид анализа часто связан с существенными инвестициями в случайные контролируемые эксперименты, хотя бывает достаточно анализа уже накопленных данных. Этот процесс может сводиться к поиску некоторого ключевого действия или события, которое меняет состояние объекта.
Достаточно распространенный пример такой задачи — определить, что именно повлияло на увеличение показателей по продажам определенного товара (это позволяет оценить эффективность вложений в рекламную кампанию).
Теперь от разговоров давай перейдем к делу. В этой статье мы подробно рассмотрим задачу регрессии на примере линейной регрессии, когда модель представляет собой линейную функцию от своих параметров. А в следующих статьях я расскажу, как решать другие задачи, возникающие в анализе данных.
Линейная регрессия
Анализ данных тесно связан с такой областью, как машинное обучение, но анализ данных — это более широкая область, включающая в себя подготовку данных и технологии обработки больших данных. В этом разделе мы рассмотрим задачу машинного обучения на примере (линейной) регрессии. Для начала давай разберемся, что же такое машинное обучение.
Если рассматривать машинное обучение с учителем (supervised machine learning), а регрессия принадлежит именно к этому классу алгоритмов, то схематично процесс можно представить с помощью рисунка.
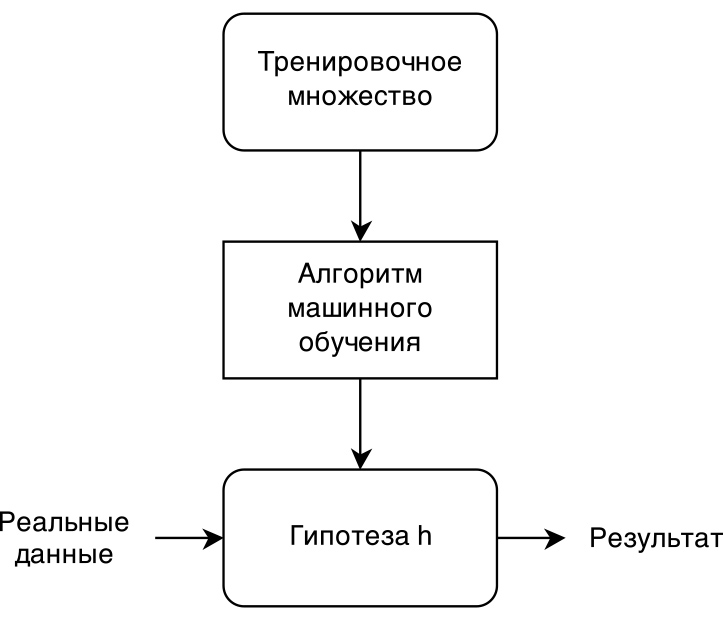
Обучающее множество передается в алгоритм машинного обучения. На основании обучающей выборки алгоритм формирует модель задачи h (иногда ее называют гипотезой, хотя это не совсем корректно). Затем полученную модель можно применять к реальным данным, но перед этим, как правило, модель проверяется на тестовом множестве.
Рассмотрим следующую задачу. Есть данные о взаимосвязи возраста и артериального давления. Да, для большинства читателей это не очень актуально, но для примера в самый раз. Тем более что наш редактор, обладатель высшего медицинского образования, всегда очень радуется, когда такие примеры проникают на страницы журнала :). Итак, у нас есть данные для 30 человек разного возраста c разным давлением.
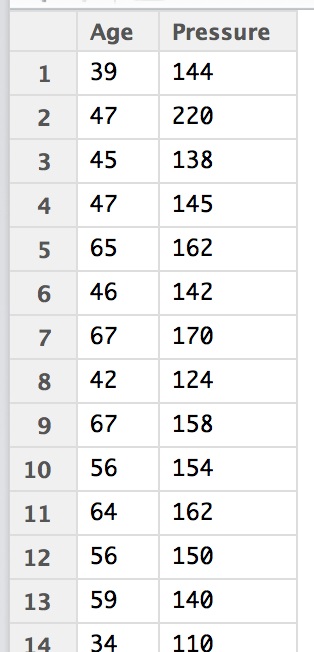
Если нанести точки из таблицы на плоскость, отложив по оси X возраст, а по оси Y давление, то можно увидеть, что большая часть точек находится вблизи некоторой гипотетической прямой. Именно потому, что это прямая, данная задача называется линейной регрессией.
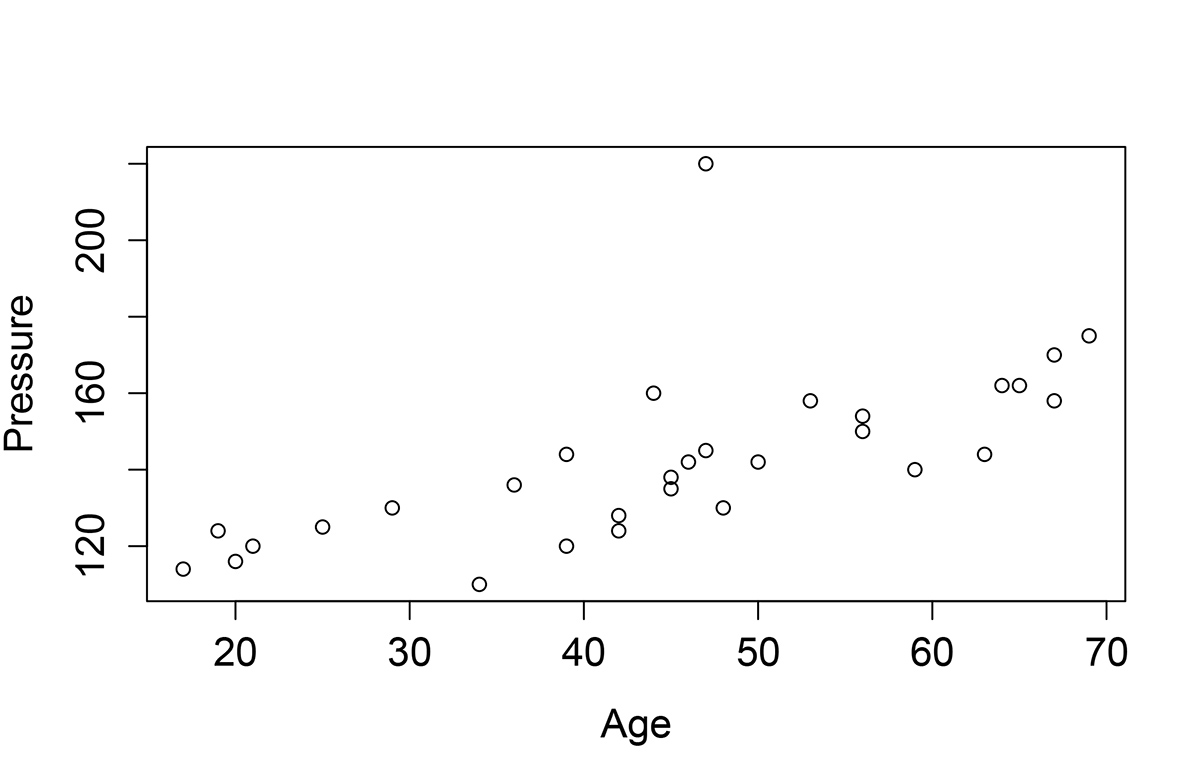
Немного теории
Давай сформулируем это более точно: в нашем случае мы ищем модель в виде линейной функции одной переменной:
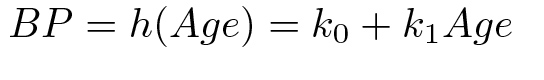
Для того чтобы найти ту самую прямую, нам необходимо подобрать коэффициенты k0 и k1 согласно какому‑то критерию. В качестве такого критерия удобно выбрать вариант метода наименьших квадратов, то есть минимизировать сумму квадратов расстояния этих точек до искомой прямой. Таким образом, мы должны минимизировать значение следующей функции относительно значений k_0 и k_1:
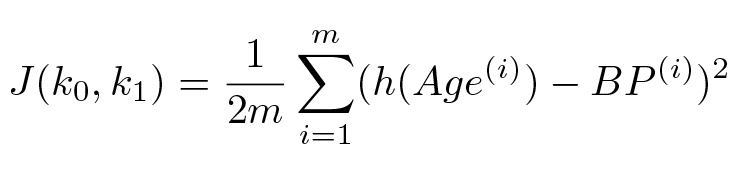
где m — это количество точек в обучающей выборке, Age и BP с верхним индексом — это соответствующие значения в i-й строке таблицы. Обычно для общности вместо Age и BP в формуле пишут просто x и y.
Как минимизировать такую функцию? Для этого воспользуемся некоторыми интуитивными соображениями. Рассмотрим для начала более простую модель g(k) = k x.
Как мы знаем еще со школы, это прямая, проходящая через центр, с тангенсом угла наклона, равным k. А как в таком случае выглядит функция J(k)? Легко проверить, что это просто парабола. В случае с двумя переменными k_0 и k_1 функция J(k_0, k_1) представляет собой эллиптический параболоид. И в том и в другом случае мы функции имеют единственный (глобальный) минимум. Найти вершину параболы учат еще в школе, но для более сложных фигур, таких как параболоид, обычно приходится использовать и более общий метод. Один из самых простых методов — это метод градиентного спуска. Для того чтобы понять, что это, потребуется знание математического анализа на уровне первого курса, а именно знание понятия частной производной. Алгоритм для градиентного спуска выглядит в общем случае следующим образом. Сначала выберем произвольные значения k_0 и k_1. Затем воспользуемся следующей итеративной процедурой:
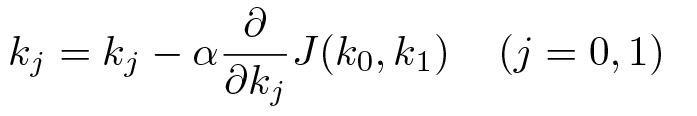
Идея алгоритма довольно простая, мы двигаемся в направлении минимизации значения искомой функции J(k_0, k_1) начиная с некоторой изначальной выбранной точки. Строго говоря, приведенный алгоритм существенно более общий и работает для нахождения локального минимума для существенно более широкого класса функций J. Однако именно в случае эллиптического параболоида и его аналогов для задач линейной регрессии большей размерности, то есть когда у нас есть не два коэффициента, а больше, наш алгоритм позволяет найти искомый глобальный минимум.
Если вычислить частную производную для нашей функции h, то мы получим следующий вариант градиентного спуска:
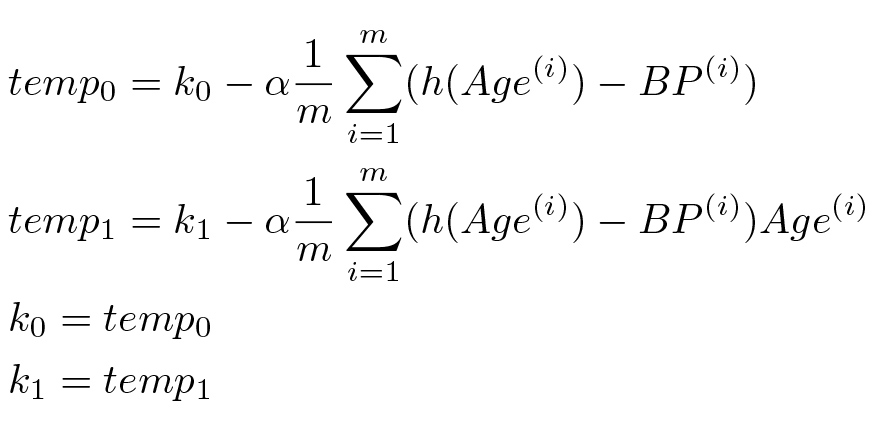
Коэффициент \alpha определяет величину шага, с которым мы двигаемся в направлении градиента функции. На практике этот шаг должен быть достаточно мал, чтобы обеспечить нужную точность, с другой стороны, он должен быть таким, что количество шагов было приемлемым с вычислительной точки зрения.
После того как найдены искомые коэффициенты, мы можем предсказать значение артериального давления для любого возраста, просто подставив в полученную формулу для h соответствующее значение возраста.
В таком виде каждый может реализовать данный алгоритм на своем любимом языке программирования, к примеру на Python. Мне кажется, это можно доверить читателю в качестве упражнения.
Если рассмотреть случай нескольких переменных, то функция h будет иметь следующий вид:
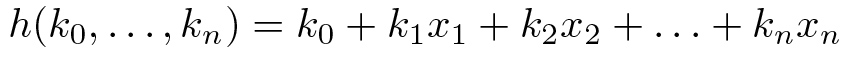
Люди, знакомые с линейной алгеброй, тут же должны заметить, что все это легко можно записать в вектором (матричном) виде. Обратим внимание, что вектор k принадлежит (n + 1)-мерному пространству, а вектор x, в свою очередь, n-мерному. Это легко поправить, дополнив вектор x координатой x_0 = 1. Тогда последнее выражение можно записать просто как h(k) =
Если пойти еще дальше, то оказывается, что задачу линейной регрессии можно решить и не прибегая к градиентному спуску. Положим, что у нас есть m строк исходных данных в таблице из n + 1 столбца (где первый столбец состоит из 1, а остальные представляют собой признаки, значения которых известны), тогда решение нашей задачи — решение так называемого нормального уравнения:
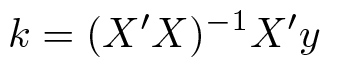
Здесь Х' — это транспонированная матрица исходных значений свойств, а y — вектор значений величины, которую мы хотим уметь вычислять для неизвестных x_1, ..., x_n. Если же матрица X' X вырождена, то есть ее определитель равен 0, то вместо обратной матрицы можно использовать псевдообратную матрицу Мура — Пенроуза.
Если использовать продвинутые средства математического моделирования, такие как MATLAB или его открытый аналог Octave, то наша задача так и будет решаться в одну строку:
pinv(X' * X) * X' * yТеперь самое время вспомнить, что за нас уже все написали. И мы можем воспользоваться существующими решениями для наших практических задач.
Практика
Существуют разные мнения о том, какие инструменты лучше всего использовать для анализа данных. Многие предпочитают связку Python/NumPy, другие используют MATLAB или Octave, кому‑то нравится хардкор, и они пишут на Haskell.
Мы не будем оригинальны и воспользуемся широко известным инструментом для работы со статистикой R, который уже давно превратился в язык общего назначения за счет бесчисленных пакетов. Следующая статья из этого цикла будет полностью посвящена использованию R для анализа данных. Здесь я лишь покажу, как решить задачу линейной регрессии без особых усилий.
Для начала нужно поставить R. Рекомендую скачивать последнюю версию R c сайта
www.r-project.org (линуксоиду на заметку: через менеджер пакетов придет не последняя версия).
В качестве среды разработки могу порекомендовать RStudio.
На самом деле установка инструментов займет у тебя существенно больше времени, чем решение нашей задачи.
Первое, что нужно сделать, — это открыть нужный CSV-файл с данными.
bp <- read.csv("age_systol.csv")Заглянуть в то, что было прочитано, можно, просто набрав название переменной, в которую данные из CSV-файла были загружены (то есть sysdata в данном случае). Для визуализации данных можно воспользоваться функцией plot.
plot(Pressure~Age, data=bp)После чего увидим распределение точек на плоскости, которое мы уже видели на рис. 2.
Теперь решим нашу задачу:
res <- lm(formula=Pressure~Age, data=bp)coefficients(res)Линейная модель содержит в себе много информации, последняя функция выводит на экран
коэффициенты линейной модели:
<!-- Результат выполнения последней операции в консоли R -->(Intercept) Age 98.7147181 0.9708704Таким образом, для нашей задачи k_0 = 98,71, а k_1 = 0,97. Мы легко можем добавить график соответствующей линейной функции прямо на последний рисунок:
abline(res, col=2)Несмотря на некоторые незначительные выбросы, наши данные очень неплохо ложатся в линейную модель, как видно на рисунке.
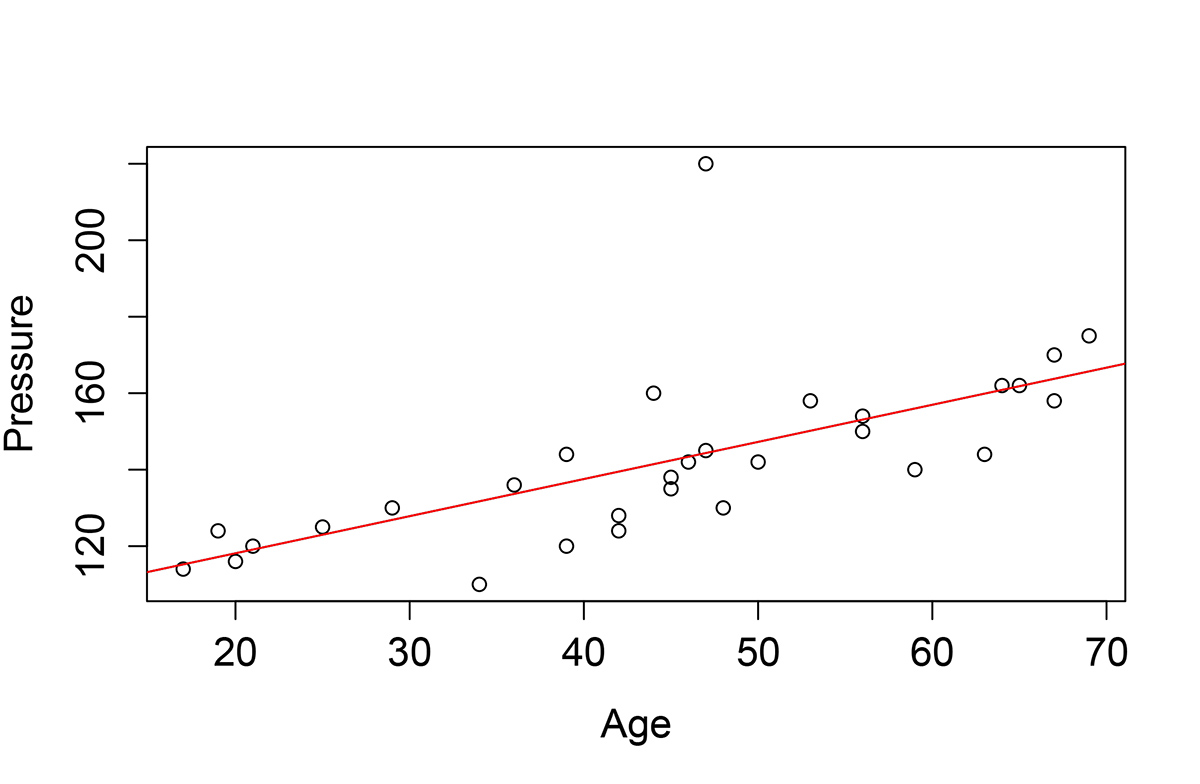
Таким образом, для любого значения возраста мы можем предсказать артериальное давление
по формуле h(.
Вместо заключения
Те, кто хочет более детально погрузиться в вопросы, связанные с линейной регрессией и машинным обучением, могут обратиться к прекрасному курсу лекций Andrew Ng, которые легко найти в интернете. Он в качестве инструмента использует Octave, а не R, однако методы остаются теми же. Ввиду ограничения размера статьи у меня не было возможности обозначить некоторые интуитивные соображения, облегчающие понимание регрессии.
Также остались за бортом многие важные аспекты, такие как масштабирование признаков (feature scaling). В тех же лекциях можно почерпнуть необходимые знания из линейной алгебры, которая хоть и в небольших количествах, но чрезвычайно полезна при анализе данных. Также настоятельно рекомендую книгу F. Provost, T. Fawcett «Data Science for Business» (O’Reilly Media, 2013). Обсуждаемый список задач, возникающих в анализе данных, как раз и был взят из этой книги. Книга доступна очень широкому кругу читателей и не требует практически никакой специальной математической подготовки.
Это была первая статья из цикла из четырех статей, посвященных анализу данных. В следующей рассказ пойдет об использовании R и визуализации данных. Третья статья будет посвящена задачам классификации и кластеризации и различным алгоритмам машинного обучения. А в последней я расскажу об инструментах обработки больших данных. В конце цикла статей обязательно сделаю список must-read книг по этой теме.



