Погружение в крипту. Часть 2: распределение ключей

Что такое шифрование без распределения ключей? Эти понятия неотделимы. В современном мире криптографии вопросу распределения ключей уделяется особое внимание, ведь злоумышленники не дремлют. Во второй части нашего ликбеза по криптографии мы доступно объясним, как работает симметричное и асимметричное шифрование, как выбрать криптостойкий ключ, зачем и как происходит распределение, а также что такое удостоверяющие центры и инфраструктура открытых ключей.

Почему распределение ключей так важно?

В нашем арсенале уже имеется несколько алгоритмов шифрования. Как и говорилось ранее, даже самые стойкие и продуманные шифры могут стать уязвимыми, если неправильно выбрать ключ шифрования или позволить украсть его злоумышленнику. Поэтому, чтобы шифрование действительно оправдало ожидания и обеспечило секретность сообщения, нужно правильно выбрать и заранее обговорить секретный ключ.

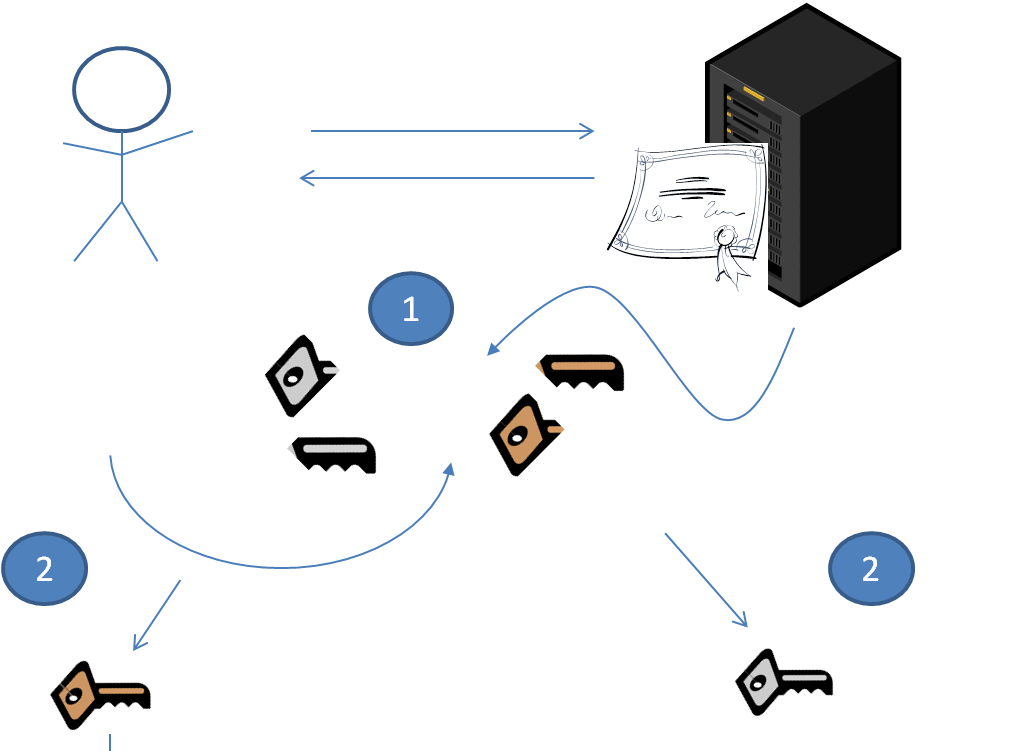
Чтобы лучше понять симметричное и асимметричное шифрование, давай представим следующую ситуацию. Ты хочешь отправить секретное сообщение с личными данными в банк. Для этого банк выдает тебе коробку и ключ. Ты кладешь письмо в коробку и закрываешь ее на ключ, банк при получении открывает эту коробку с помощью аналогичного ключа. Такой метод является симметричным, так как обе стороны используют один и тот же ключ расшифрования. Однако злоумышленник может перехватить ключ и открыть коробку. Чтобы это предотвратить, банк поступает хитрее: он предоставляет тебе коробку и навесной замок, а единственный ключ банк хранит у себя. Таким образом, воспользоваться замком может кто угодно, но открыть коробку может только обладатель ключа. Такой подход называется асимметричным: замок играет роль открытого (публичного) ключа, а ключ банка — секретного (приватного).

Симметричное шифрование предусматривает шифрование и расшифрование с помощью одного и того же секретного ключа, поэтому пользователям важно правильно выработать совместный ключ, а также безопасно его передать. В условиях незащищенного канала это сделать очень сложно. Асимметричное шифрование как раз решает эту проблему: операции шифрования и расшифрования осуществляются с помощью разных ключей (открытого и секретного). В этом случае обладателю пары ключей необходимо передать собеседнику только открытый ключ, единственного назначение которого — необратимо зашифровать информацию, расшифровать которую сможет только получатель с помощью приватного ключа.

-----------------------------
        | З | А | Б | Е | Г |
-----------------------------
№ буквы | 9 | 1 | 2 | 6 | 4 |
-----------------------------

--------------------------------------
(№ буквы)^3 | 729 | 1 | 8 | 216 | 64 |
--------------------------------------

---------------------------------------
(№ буквы)^3 mod10 | 9 | 1 | 8 | 6 | 4 |
---------------------------------------

------------------------------------------
(код)^3       | 729 | 1 | 512 | 216 | 64 |
------------------------------------------
(код)^3 mod10 | 9   | 1 | 2   | 6   | 4  |
------------------------------------------
буква         | З   | А | Б   | Е   | Г  |
------------------------------------------

В случае симметричного шифрования перед собеседниками всегда стоят две важные задачи:

• выбор криптостойкого ключа;
• распределение ключа (надежный обмен).

В случае асимметричного шифрования возникает другая задача:

• обмен собеседников открытыми ключами.

Иными словами, Алиса, обладая открытым ключом Боба, не может быть уверена на 100%, что этот ключ принадлежит именно Бобу.

Начнем с первого случая.

Выбор криптостойкого ключа

Стоит сразу раскрыть главный критерий стойкого ключа в симметричном шифровании: он должен быть случайным. Например, стойкость симметричного шифра Вернама напрямую зависит от выбора ключа. Чем меньше связь между символами ключа, чем больше его длина, тем выше его криптостойкость. В идеале ключ представляет собой абсолютно случайную последовательность с длиной не меньшей, чем у шифруемого текста. Такая длина необходима для того, чтобы исключить возможность брутфорса. К примеру, пин-коды банковских карт (состоящие всего из 4 цифр) от такой атаки защищает только ограничение банка на количество попыток ввода пароля; убери это ограничение, и подбор любого пин-кода займет не более пары часов.

В современных системах, чтобы сгенерировать случайную последовательность для ключа, применяют различные подходы. Стандартные UNIX утилиты random и urandom хэшируют данные, снимаемые со счетчика тактов процессора во время аппаратных прерываний. Microsoft Crypto API берет хэш от внутреннего состояния компьютера — текущего времени, размера жесткого диска, размера свободной памяти, номера процесса и так далее. В ход также идут всевозможные случайные данные. Например, в процессе оцифровки звукового сигнала на линейный вход звуковой карты приходит аналоговый электрический сигнал, который содержит шум, состоящий из:

• радиопомех и наводок от соседних устройств и радиоэфира;
• помех электропитания;
• теплового шума случайного движения электронов в компонентах электрической схемы.

Используется и квантовый шум, который носит истинно случайный характер. Квантовый шум «проникает» в цифровую часть звуковой карты, где его можно сразу и использовать. Также нередко прибегают к помощи пользователя, требуя набирать случайные символы на клавиатуре, двигать мышкой, пока идет генерация сигнала, или произносить определенные слова.

Теперь немного о времени жизни ключа. Для нас этот показатель очень важен — ведь чем дольше ключ находится в обращении, тем легче злоумышленнику его получить и тем большую ценность этот ключ для него представляет. С самого момента генерации секретного ключа нужно задуматься, как часто его нужно менять. Кроме того, важный момент — уничтожение секретного ключа. Если речь идет о сессионном ключе, его стоит безвозвратно уничтожить сразу по окончании сеанса связи. Если речь о долговременном — пусть живет указанный срок, но, опять же, ни секундой дольше.

Сессионные ключи, несмотря на их недолгий срок службы, играют важную роль. Они используются повсеместно, начиная от защищенной TLS сессии и заканчивая прикладными программами (например, мессенджерами). Также сессионные ключи применяются при входе в личный кабинет интернет-банка и иных подобных сервисах, где речь идет об особо важных данных и ключи важно менять как можно чаще.

Распределение ключей (надежный обмен ключами)

Другой важной задачей симметричной криптографии помимо выбора суперстойкого ключа является распределение ключей — надежный и защищенный от перехвата способ обмена ключами.

При симметричном шифровании и выработке совместного ключа со своим товарищем сложные схемы ни к чему — можно использовать простой алгоритм Диффи-Хеллмана:

1. Я и мой товарищ знаем два абсолютно несекретных числа g и p. Я придумываю большое число a, а мой товарищ большое число b.
2. Я вычисляю A = g^a mod p и отправляю товарищу.
3. Товарищ вычисляет B = g^b mod p и отправляет мне.
4. Я вычисляю B’ = B^a mod p = g^(ab) mod p.
5. Товарищ вычисляет A’ = A^b mod p = g^(ab) mod p.

В итоге, A’ = B’ и есть согласованный ключ.

Рассмотрим пример на небольших числах. Пусть g = 2, p = 100, мое число a = 4, а число товарища b = 2:

A = 2^4 mod 100 = 16
B = 2^2 mod 100 = 4
A’ = B^a =4^4 mod 100 = 56
B’ = A^b = 16^2 mod 100 = 56

Если использовать достаточно большие числа a, b и p, шансов получить ключ у злоумышленника будет очень мало.

Протокол Диффи-Хеллмана в чистом виде сейчас, разумеется, нигде не используется. Однако многие протоколы аутентификации построены на его основе: модификации обмена ключами Диффи-Хеллмана можно встретить и в сетевых протоколах, таких как IPSec и TLS, и в отдельных криптографических приложениях.

А как передать ключ?

На первый взгляд, очевидно, физическим способом — нанять курьера и приставить к нему охрану. Или, например, отправить по почте России письмом первого класса. Послать сову, в конце концов. Вариантов много. Однако, если у вас не один друг или не один пользователь криптографической системы, такой метод невыгоден и неудобен. А уж если кто-то из них живет, например, в Австралии, ждать ему придется довольно долго. В масштабах современного мира такой вариант все еще возможен, но абсолютно неудобен. Криптографы долго думали, как избавиться от курьера, и решили, что неплохо было бы разработать специальные протоколы для распределения ключей.

Для знакомства с протоколами распределения ключей представим, что некой криптографической системой пользуются несколько участников. Они договорились о том, как должен выглядеть ключ шифрования, и каждый генерирует его для себя особым методом. Но тут один пользователь сказал другому (по секрету), что в системе есть нечестный участник. Каждый пользователь начал подозревать своих товарищей... и в результате ключами больше никто не обменивается.

Для решения этой проблемы — общения в условиях недоверенности — большинство протоколов распределения ключей предусматривает наличие «центра доверия». Обычно это некий центральный сервер, которому доверяют все пользователи, используя его для получения ключей и обмена ими между собой при необходимости. Конечно, если есть возможность обменяться ключами напрямую по абсолютно доверенному протоколу, будучи уверенным, что ключ принадлежит именно твоему собеднику, можно обойтись и без УЦ. В реальной жизни такие ситуации, к сожалению, почти не встречаются.

Далее в тексте мы будем рассматривать только протоколы, в которых участники сообщаются единым центром доверия.

Протокол широкоротой лягушки

Первым протоколом для обмена секретными ключами в симметричных криптосистемах, с которым мы познакомимся, будет протокол широкоротой лягушки. Рассмотрим его на примере пользователей A и B, которые хотят обменяться ключами друг с другом. Каждый из них для связи с центром доверия S имеет ключ Ka и Kb соответственно. Порядок действий будет выглядеть следующим образом.

1. А генерирует ключ K для связи с В и отправляет в центр доверия сообщение (K,T), зашифрованное на его ключе Ka (где Т — временная метка).
2. Сервер проверяет временную метку и расшифровывает сообщение, если метка соответствует текущему времени.
3. S шифрует ключ K на ключе Kb, прикрепляет временную метку и отправляет B.
4. B получает сообщение, проверяет метку и извлекает ключ K.

Другие статьи в выпуске:

Xakep #206. Ключ от всех дверей

• Содержание выпуска
• Подписка на «Хакер»-60%

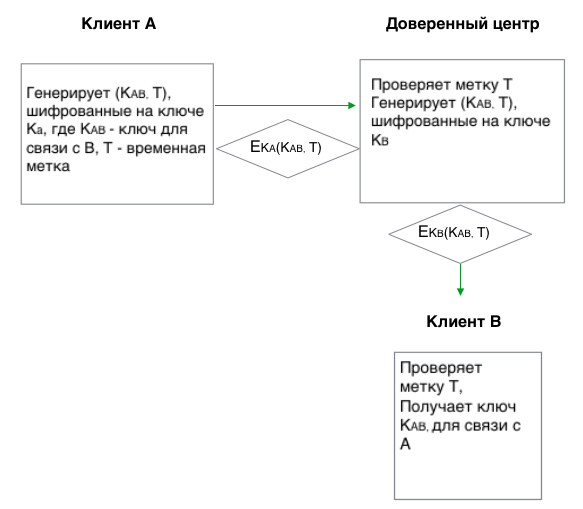
Протокол очень прост и основан на синхронизации часов всех участников, за которую несет ответственность доверенный центр. Однако на практике этот протокол используется мало, потому что ответственность за генерацию сессионного ключа лежит на плечах самих участников, а кто знает, что они там нагенерируют?

Протокол широкоротой лягушки использует концепцию единого центра доверия. Такой подход к управлению ключами применим и для асимметричной криптографии. Удостоверяющий центр лежит в основе известной и самой используемой на данный момент инфраструктуры управления открытыми ключами — PKI.

Инфраструктура открытых ключей (PKI)

Приступим к основной проблеме в асимметричном шифровании — как узнать наверняка, кому принадлежит открытый ключ. Решением этой задачи является инфраструктура открытых ключей, с которой мы сейчас и разберемся.

Что же это за инфраструктура такая? PKI (Public Key Infrastructure) — это современная система управления криптографической защитой, в том числе и в среде, которая кишит злоумышленниками (например, в интернете). Инфраструктура открытых ключей оперирует понятием «сертификата», который содержит открытый ключ пользователя и идентифицирующую этого пользователя информацию. Задачей PKI является определение политики выпуска электронных сертификатов: их выдача, аннулирование и хранение информации, необходимой для последующей проверки правильности сертификатов. В число приложений, поддерживающих PKI, входят: защищенная электронная почта, протоколы платежей, электронные чеки, электронный обмен информацией, защита данных в сетях с протоколом IP, электронные формы и документы с электронной цифровой подписью. Одним словом, куда в интернете не глянь — наткнешься на PKI.

Ты приходишь в доверенный центр и получаешь сертификат (иначе говоря, открытый ключ), который можешь использовать по назначению. Далее ты отправляешь этот сертификат своим товарищам, чтобы они могли подтвердить твою личность. В этом сертификате указывается время получения, время истечения сертификата и информация о владельце. Подразумевается, что сертификат ты будешь предъявлять до тех пор, пока не истечет указанный срок. PKI предусматривает как документацию, так и набор прикладных программ для управления сертификатами. Документация определяет необходимый жизненный цикл каждого сертификата — время жизни, условия отзыва, хранение, передачу. Прикладные программы, в свою очередь, реализуют манипуляции с сертификатами на практике. Чтобы посмотреть пример сертификата, можно обратиться к сетевым протоколам, аутентификация в которых происходит зачастую как раз на основе сертификатов PKI.

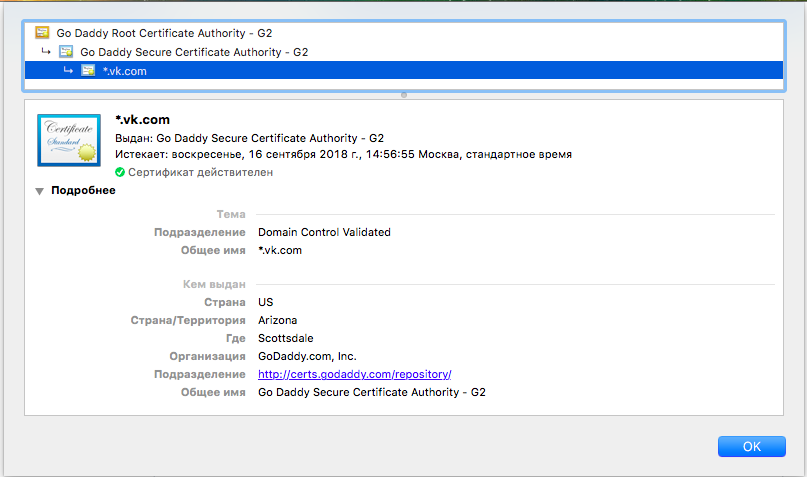
При любом подключении к сайту по https наш браузер проверяет сертификат, смотрит на время истечения и только тогда разрешает защищенное соединение.

INFO

Если тебе интересно, как работать с PKI на прикладном уровне, обязательно прочти статью «Открытые ключи для серьезных пацанов» в рубрике «КОДИНГ» этого номера. В статье показано, как реализовать на C# основные операции: проверку подписи, шифрование и расшифрование в контексте PKI.

Kerberos

В 1987 г в Массачусетском технологическом институте был разработан еще один интересный протокол аутентификации: Kerberos. Сейчас эта система общедоступна и ее реализации используются в различных операционных системах, в том числе и в Windows, как метод аутентификации пользователей в домене. Существует несколько open source реализаций протокола Kerberos: например, оригинальная MIT Kerberos и Heimdal. Такое многообразие возникло из-за ограничений США на экспорт криптографических средств защиты информации. На сегодняшний день волнения вокруг MIT Kerberos уже улеглись.

Суть Kerberos состоит в следующем. Предполагается, что компьютерная сеть состоит из клиентов и сервера, причем клиентами могут быть программы и специальные службы. Kerberos хранит центральную базу данных, включающую как клиентов, так и их секретные ключи, на центральном сервере, который называется KDC (Key Distribution Center). Цель системы — идентификация клиентов и генерирование для них сеансовых ключей.

Как это работает?

Предположим, клиент A хочет получить доступ к ресурсам клиента B.

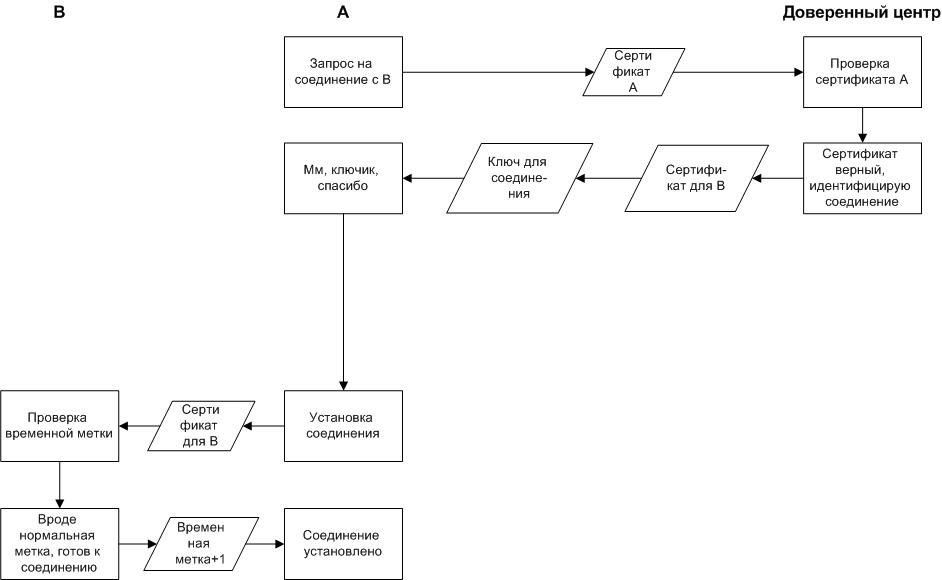
1. A заходит на сервер аутентификации Kerberos, используя свой пароль.
2. Сервер выдает ему сертификат, зашифрованный с помощью этого пароля. Сертификат содержит сеансовый ключ К.
3. А использует К для получения второго сертификата, предназначенного для установления соединения с В. У второго сертификата обозначено время жизни и временная метка, он зашифрован на ключе B.
4. Чтобы убедиться в том, что сертификат валидный, А отправляет В зашифрованную на сеансовом ключе временную метку.
5. B проверяет метку, инкрементирует ее и отправляет A (опять же шифруя на сеансовом ключе), таким образом подтверждая, что тоже имеет ключ доверенного центра и готов к сеансу связи.
6. А предъявляет свой сертификат B. B расшифровывает сертификат, проверяет его и подтверждает установку соединения.

Систему Kerberos версии 5 поддерживает множество Unix-подобных систем: FreeBSD, Apple's Mac OS X, Red Hat Enterprise Linux, Oracle's Solaris, IBM's AIX и Z/OS и так далее. При желании можно настроить аутентификацию Kerberos 5 внутри сети организации с использованием смарт-карт или сертификатов. Kerberos можно нередко встретить там, где происходит аутентификация в сети: так, например, Windows использует Kerberos при аутентификации в Active Directory и защищенном обновлении DNS адресов. IP-sec хосты тоже порой аутентифицируют друг друга через Kerberos.

Заключение

Правильный ключ — это главная проблема криптографии. Нужно всегда помнить, что даже самый стойкий шифр потеряет смысл, если не подумать о случайности, длине, времени жизни и распределении ключа.

В следующих статьях мы рассмотрим шифры, в которых применяются сертификаты PKI и открытые ключи.