Код Хаффмана. Как распаковать таблицы, сжатые Huffman Encoding, в Intel ME 11.x

Предыдущие версии ME

Ознакомившись с исходными текстами, являющимися частью проекта unhuffme, легко увидеть, что для предыдущих версий ME существует два набора таблиц Хаффмана и в каждом из наборов присутствует две таблицы. Наличие двух таблиц (по одной для кода и для данных) обусловлено, вероятно, тем, что статистические свойства кода и данных сильно отличаются.

Также примечательны следующие свойства:

• Для разных наборов таблиц диапазоны длин кодовых слов различаются (7–19 и 7–15 бит включительно).
• Каждая кодовая последовательность кодирует целое количество байтов (от 1 до 15 включительно).
• В обоих наборах используется Canonical Huffman Coding (это позволяет быстро определять длину очередного кодового слова при распаковке).
• В пределах одного набора длины закодированных значений для любого кодового слова совпадают во всех таблицах (Code и Data).

Постановка задачи

Можно предположить, что в таблицах Хаффмана для ME 11.x три последних свойства также соблюдаются. Тогда для полного восстановления таблиц требуется найти следующее:

• диапазон длин кодовых слов;
• границы значений кодовых слов, имеющих одинаковую длину (Shape);
• длины закодированных последовательностей для каждого кодового слова;
• закодированные значения для каждого кодового слова в обеих таблицах.

Разбиение сжатых данных на отдельные страницы

Для получения информации об отдельных модулях можно использовать имеющиеся знания о внутренних структурах прошивки.

Разобрав Lookup Table, часть Code Partition Directory, легко определить, для каких модулей применяется кодирование Хаффмана, где начинаются их упакованные данные и какой размер модуль будет иметь после распаковки.

Размер сжатых и распакованных данных и SHA-256 от распакованных данных несложно найти, разобрав Module Attributes Extension для конкретного модуля.

Беглый анализ нескольких прошивок для ME 11.x позволяет заметить, что размер данных после распаковки Хаффманом всегда кратен размеру страницы (4096 == 0x1000 байт). В начале упакованных данных располагается массив четырехбайтовых целочисленных значений. Количество элементов массива соответствует количеству страниц в распакованных данных.

Например, для модуля размером 81920 == 0x14000 байт массив будет занимать 80 == 0x50 байт и состоять из 20 == 0x14 элементов.

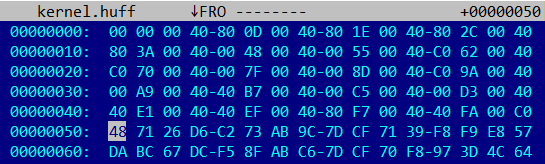
В двух старших битах каждого из Little-Endian-значений хранится номер таблицы (0b01 для кода и 0b11 для данных). В оставшихся 30 битах хранится смещение начала сжатой страницы относительно конца массива смещений. Приведенный выше фрагмент описывает 20 страниц:

Примечательно, что смещения упакованных данных для каждой страницы отсортированы по возрастанию, а размер упакованных данных для каждой страницы в явном виде нигде не фигурирует. В приведенном выше примере упакованные данные для каждой конкретной страницы начинаются на границе, кратной 64 = 0x40 байтам, а неиспользуемые области заполнены нулями. Но по другим модулям можно установить, что выравнивание не обязательно. Это наталкивает на мысль, что распаковщик останавливается, когда объем данных распакованной страницы достигает 4096 байт.

Так как мы знаем общий размер упакованного модуля (из Module Attributes Extension), мы можем разделить упакованные данные на страницы и работать с каждой отдельно. Начало упакованной страницы определяется из массива смещений, а размер — смещением начала следующей страницы или общим размером модуля. При этом после упакованных данных может идти произвольное количество незначащих бит (эти биты могут иметь любые значения, но на практике они обычно нулевые).

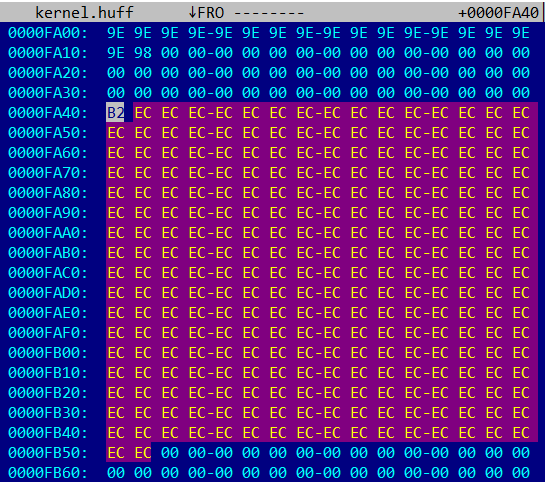
На скриншоте видно, что последняя сжатая страница (начинающаяся по смещению 0xFA40) состоит из байта 0xB2 == 0b10110010, за которым идет 273 байта со значением 0xEC == 0b11101100, и дальше — только нули. Так как битовая последовательность 11101100 (или 01110110) повторяется 273 раза, можно предположить, что она кодирует 4096/273 == 15 одинаковых байт (скорее всего, со значениями 0x00 или 0xFF). Тогда битовая последовательность 10110010 (или 1011001) кодирует 4096-273*15 == 1 байт.

Это хорошо согласуется с предположением о том, что каждая кодовая последовательность кодирует целое количество байтов (от 1 до 15 включительно). Однако полностью восстановить таблицы Хаффмана таким образом невозможно.

Нахождение пар «сжатый текст — открытый текст»

Как было показано ранее, в разных версиях прошивок для ME 11 модули с одинаковыми названиями могут упаковываться разными алгоритмами. Если разобрать Module Attributes Extension для одноименных модулей, упакованных как LZMA, так и Хаффманом, и извлечь значения SHA-256 для каждого модуля, то не обнаружится ни одной пары модулей, упакованных разными алгоритмами и имеющих одинаковые значения хешей.

Но если вспомнить, что для модулей, упакованных LZMA, SHA-256 обычно считается от сжатых данных, и посчитать SHA-256 для модулей после распаковки LZMA, то обнаружится достаточно много подходящих пар. И для каждого такого «парного» модуля мы сразу получим несколько пар страниц — в упакованном Хаффманом и распакованном виде.

Продолжение доступно только участникам

Вариант 1. Присоединись к сообществу «Xakep.ru», чтобы читать все материалы на сайте

Членство в сообществе в течение указанного срока откроет тебе доступ ко ВСЕМ материалам «Хакера», позволит скачивать выпуски в PDF, отключит рекламу на сайте и увеличит личную накопительную скидку! Подробнее

-60% 1 год 9990 рублей 4000 р.

1 месяц 920 р.

Вариант 2. Открой один материал

Заинтересовала статья, но нет возможности стать членом клуба «Xakep.ru»? Тогда этот вариант для тебя! Обрати внимание: этот способ подходит только для статей, опубликованных более двух месяцев назад.

Я уже участник «Xakep.ru»