Содержание статьи
Сегодня я немного расскажу о решении задачи классификации с использованием программного пакета R и его расширений. Задача классификации, пожалуй, одна из самых распространенных в анализе данных. Существует множество методов для ее решения с использованием разных математических техник, но нас с тобой, как апологетов R, не может не радовать, что при этом программировать что-либо с нуля не нужно, — все есть (причем далеко не в единственном экземпляре) в системе пакетов R.
Задача классификации
Задача классификации — типичный пример «обучения с учителем». Как правило, мы располагаем данными в виде таблицы, где столбцы содержат значение наборов признаков для каждого случая. Причем все строки заранее размечены таким образом, что один из столбцов (положим, что последний) указывает на класс, к которому принадлежит данная строка. Как хороший пример можно привести задачу классификации писем на спам и не спам. Для того чтобы воспользоваться алгоритмами машинного обучения, нужно для начала иметь размеченные данные — такие, для которых значение класса известно наряду с остальными признаками. Причем набор данных должен быть существенным, особенно если количество признаков велико.
Если у нас есть достаточно данных, то можно начинать обучение модели. Общая стратегия с классификаторами не особо зависит от модели и включает следующие шаги:
- выбор тренировочного и тестового множества;
- обучение модели на тренировочном множестве;
- проверка модели на тестовом множестве;
- перекрестная проверка;
- улучшение модели.
Точность и полнота
Как оценить, насколько хорошо работает наш классификатор? Непростой вопрос. Дело в том, что различные варианты развития событий возможны, даже если у нас есть всего только два класса. Допустим, мы решаем задачу фильтрации спама. После проверки модели на тестовом множестве мы получим четыре величины:
TP (true positive) — сколько сообщений было правильно классифицировано как спам,
TN (true negative) — сколько сообщений было правильно классифицировано как не спам,
FP (false positive) — сколько сообщений было неправильно классифицировано как спам (то есть письма спамом не были, но модель классифицировала эти сообщения как спам),
FN (false negative) — сколько сообщений было неправильно классифицировано как не спам, а на самом деле это был все-таки Центр американского английского.
В зависимости от деталей решаемой задачи качество модели может быть оценено по-разному. В каждом конкретном случае нам нужно выбрать, что важнее: чтобы в спам попало как можно больше писем, которые на самом деле являются спамом, и мы готовы пожертвовать некоторыми важными сообщениями или же чтобы в спам попадали только гарантированно «плохие» сообщения, а все остальные сообщения терялись в папке спам как можно реже (наверное, у всякого приличного интернетчика хотя бы раз в жизни важное-важное сообщение пропадало в спаме). Редко удается усидеть на двух стульях, и поэтому приходится при выборе классификатора принять решение в пользу той или иной стратегии. Как правильно отразить эти два крайних случая с математической точки зрения? Математической реализацией этих двух случаев служат точность (precision) и полнота (recall) соответственно. Это сравнительно простые характеристики модели, которые определяются следующим образом:
- точность
PPV = TP / (TP + FP); - полнота
TPR = TP / (TP + FN).
Иногда хочется иметь величину, которая бы показывала качество модели в целом, учитывая и точность и полноту. Для этого можно использовать так называемую F-меру:
F1 = 2*TP / (2*TP + FP + FN)F-мера представляет собой гармоническое среднее между точностью и полнотой. Это означает, что если хотя бы одна из этих двух величин стремится к нулю, то и F-мера стремится к нему же. На самом деле описанный вариант учитывает и точность, и полноту в равной степени, однако можно корректировать значимость каждой из величин (см. формулу 1).
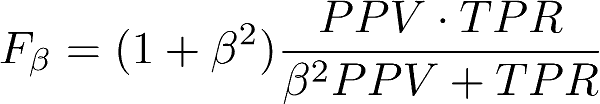

Xakep #198. Случайностей не бывает
Эффект переобучения
Бывает, модель «выучивает» те свойства обучающего множества, которые не характерны для данных в общем случае, как иногда говорят — отсутствуют в генеральной совокупности. Такая модель на реальных данных будет давать плохие результаты. Этот феномен известен как переобучение, или overfitting. Способы борьбы с переобучением зависят от алгоритма машинного обучения. К примеру, для деревьев решений от эффекта переобучения можно избавиться за счет отсечения некоторых ветвей (см. далее).
Перекрестная проверка
Перекрестная проверка, или cross-validation, — это всего лишь метод проверки модели. Очень часто данные делят тренировочное и тестовое множество в соотношении 2 : 1. Таким образом, обучают модель на 2/3 данных, а тестируют на 1/3. А что будет, если с данными что-то не так? И как понять, что модель ведет себя неправильно? Для того чтобы убедиться, что модель работает хорошо, поступают следующим образом: данные делятся на k частей, из этих частей (k – 1) используется для обучения модели, а одна для тестирования. Процедура повторяется k раз, так, чтобы каждый из семплов использовался для тестирования ровно один раз. Такой способ перекрестной проверки известен как k-fold. Часто используется 10-fold, но на самом деле нет никаких специальных ограничений на k.
Каждый легко может представить и другие виды перекрестной проверки, решающие ту же самую задачу. В целом все методы можно поделить на исчерпывающие (exhaustive) и неисчерпывающие (non-exhaustive). Первые проверяют все возможные варианты для обучения/тестирования, а вторые — лишь часть. Ко второму классу можно отнести методы со случайной выборкой типа Монте-Карло. Очевидно, что k-fold относится к исчерпывающим методам. Его можно усложнить, сделав разбиение на (k – p) и p семплов соответственно.
Деревья решений
Теперь можно приступить к практике. Начнем с чего-нибудь интуитивно понятного.
Для начала нужно выбрать данные, с которыми мы планируем работать. В интернете можно найти огромное количество данных для анализа и обработки, но так как цель этой статьи сугубо обучающая, то мы воспользуемся классическим источником: существует прекрасная книга An Intoduction to Statistical Learning with Application with R, которую легко найти в интернете. Для R есть специальный пакет ISLR, нужно будет установить его перед работой. Также нам понадобится пакет tree, в котором реализован алгоритм работы с деревьями решений (на самом деле это далеко не единственный пакет для подобных задач, чуть позже мы рассмотрим и другие варианты). Для начала подключаем все это хозяйство:
library(ISLR)
library(tree)
head(Carseats)
attach(Carseats)Здесь мы будем работать с данными Carseats из пакета ISLR, это учебный материал по продажам автокресел в 400 различных магазинах. Для начала посмотрим, что представляет собой этот набор данных:
Sales CompPrice Income Advertising Population Price ShelveLoc Age Education Urban US
1 9.50 138 73 11 276 120 Bad 42 17 Yes Yes
2 11.22 111 48 16 260 83 Good 65 10 Yes Yes
3 10.06 113 35 10 269 80 Medium 59 12 Yes Yes
4 7.40 117 100 4 466 97 Medium 55 14 Yes Yes
5 4.15 141 64 3 340 128 Bad 38 13 Yes No
6 10.81 124 113 13 501 72 Bad 78 16 No YesС помощью attach мы делаем колонки обычными переменными, то есть вместо того, чтобы писать каждый раз Carseats$Sales, теперь можно просто указывать Sales, что несомненно удобно. Положим, мы хотим просто разделить все продажи на высокие и низкие, а затем понять, как признаки в нашей таблице влияют на качество продаж. Подробное описание формата данных можно получить обычным способом, просто набрав ?Carseats в консоли R.
Сперва надо решить, что считать высокими, а что низкими продажами. Сначала можно посмотреть, в каком промежутке меняются значения Sales во всем объеме данных:
range(Sales)
[1] 0.00 16.27Положим, что продажи можно считать большими, если значение больше или равно 8. Отразим это, добавив соответствующий столбец к нашему фрейму данных. Чтобы его создать, можно воспользоваться векторной функцией ifelse:
High = ifelse(Sales >= 8, "Yes", "No")Так мы получили отдельный вектор из Yes и No. Теперь его легко присоединить к нашему фрейму данных Carseats. Строго говоря, колонка Sales нам больше не нужна, и ее можно просто удалить:
Carseats = Carseats[, -1] # Удаляем Sales
Carseats = data.frame(Carseats, High) # Добавляем HighПеред тем как разбить данные на тестовое и тренировочное множество, было бы неплохо зафиксировать начальное значение генератора случайных чисел:
set.seed(3)Это сделает наши результаты воспроизводимыми. Если, к примеру, качество данных плохое, то при построении и тестировании модели точность и F-мера могут значительно различаться, что может быть нежелательно. Теперь разделим наши данные на тренировочное и тестовое множества в отношении 2 : 1. Это можно сделать с помощью функции sample:
n = nrow(Carseats)
test = sample(1:n, n/3)
train = -testТеперь test — это вектор случайных чисел от 1 до n длины n/3. Так как удалять колонки и строки можно, просто используя отрицательные значения индексов, то тренировочное и тестовое множество будут выглядеть следующим образом:
training_set = Carseats[train, ]
testing_set = Carseats[test, ]Для того чтобы обучить модель, достаточно всего лишь одного вызова:
tree_model = tree(High~., training_set)Здесь High~. представляет собой формулу, которая говорит системе, что переменная High зависит от всех признаков. Иногда бывает полезно визуализировать модель. Это можно сделать с помощью стандартной функции plot:
plot(tree_model)Результатом работы такой функции будет отрисованное дерево решений. В таком виде оно довольно бесполезно, поэтому соответствующие ветвления нужно подписать:
text(tree_model)Результат выполнения команды plot изборажен на Рис 1.
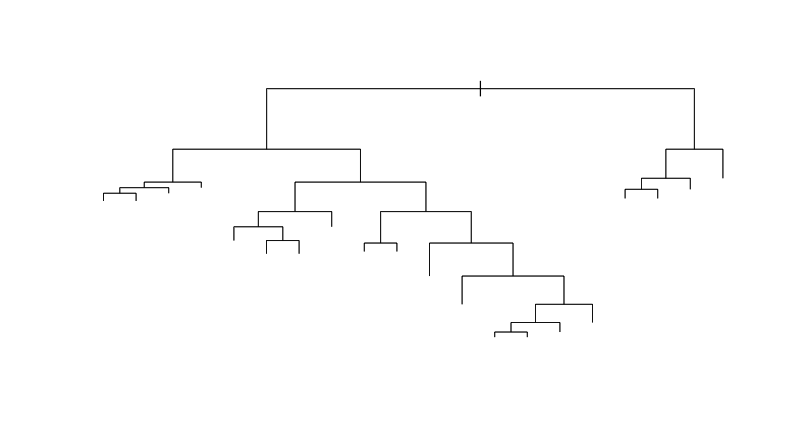
Посмотри на дерево, и тебе станет понятно, что происходит. Алгоритм дает нам просто набор условных выражений, посредством которых происходит классификация. Теперь можно преступить к проверке модели. Для начала попробуем модель на тестовых данных:
tree_pred = predict(tree_model, testing_set, type="class")
mean(tree_pred != High[test])Здесь первая строчка строит предсказание на основе модели для тестового множества, type=class указывает на то, что мы занимаемся задачей классификации. Наверное, самым простым способом проверки модели является простой подсчет ошибок — функция mean даст нам количество ошибок в долях от единицы. Здесь это значение равно 0.2481203, что в переводе на русский язык означает 24.8%.
Кстати, как насчет улучшения результата? Если внимательно посмотреть на дерево решений, можно предположить, что мы имеем дело с переобучением: некоторые закономерности, которые стали частью модели, на самом деле не свойственны тестовому множеству. В случае деревьев это, как правило, означает, что высота дерева слишком велика и нужно удалить лишние ветки.
А как определить, сколько именно ветвей нужно удалять? В этом деле нам поможет процедура перекрестной проверки. Средствами R она реализуется довольно легко:
set.seed(5)
cv_tree = cv.tree(tree_model, FUN=prune.misclass)В этом (достаточно понятном и без всяких комментариев) коде мы сначала еще раз устанавливаем начальное значение для генератора псевдослучайных чисел. Затем с помощью встроенной функции мы делаем перекрестную проверку. Результатом будет список cv_tree, в котором есть поля size и dev: первое - размер дерева (его высота), второе - допуск ошибки. Функция prune.misclass - как раз та функция, которая позволит нам сделать отсечение:
plot(cv_tree$size, cv_tree$dev, type="b")Если посмотреть на построенный график зависимости ошибки от размера дерева (см. рис. 2), то видно, что минимум ошибки приходится где-то на 9:
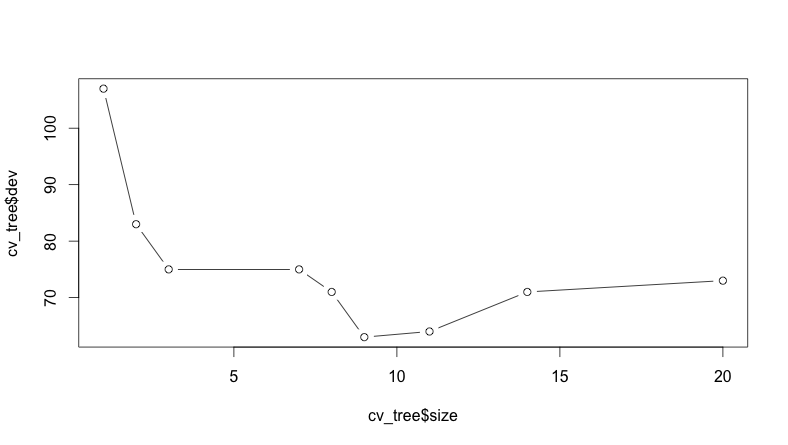
Исходя из полученных данных, можно сделать улучшенную модель, сделав отсечение ветвей с помощью той же функции (см. рис. 3):
prune_model = prune.misclass(tree_model, best=9)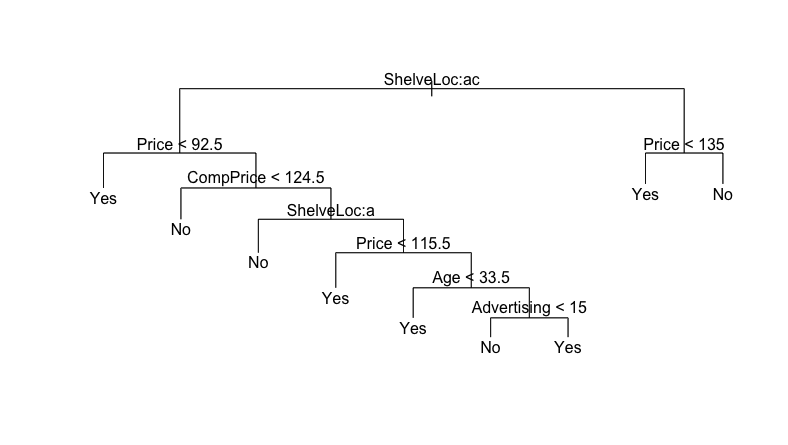
Часто бывает нужно визуализировать дерево решений прямо в консоли. Для этого достаточно просто напечатать модель:
print(prune_model)
node), split, n, deviance, yval, (yprob)
* denotes terminal node
1) root 267 359.500 No ( 0.59925 0.40075 )
2) ShelveLoc: Bad,Medium 213 260.400 No ( 0.69953 0.30047 )
4) Price < 92.5 30 36.650 Yes ( 0.30000 0.70000 ) *
5) Price > 92.5 183 199.500 No ( 0.76503 0.23497 )
10) CompPrice < 124.5 79 42.460 No ( 0.92405 0.07595 ) *
11) CompPrice > 124.5 104 135.400 No ( 0.64423 0.35577 )
22) ShelveLoc: Bad 34 15.210 No ( 0.94118 0.05882 ) *
23) ShelveLoc: Medium 70 97.040 Yes ( 0.50000 0.50000 )
46) Price < 115.5 19 7.835 Yes ( 0.05263 0.94737 ) *
47) Price > 115.5 51 64.920 No ( 0.66667 0.33333 )
94) Age < 33.5 8 0.000 Yes ( 0.00000 1.00000 ) *
95) Age > 33.5 43 44.120 No ( 0.79070 0.20930 )
190) Advertising < 15 37 25.350 No ( 0.89189 0.10811 ) *
191) Advertising > 15 6 5.407 Yes ( 0.16667 0.83333 ) *
3) ShelveLoc: Good 54 54.590 Yes ( 0.20370 0.79630 )
6) Price < 135 46 27.180 Yes ( 0.08696 0.91304 ) *
7) Price > 135 8 6.028 No ( 0.87500 0.12500 ) *Теперь можно опять проверить работоспособность нашей модели на тестовых данных:
tree_pred1 = predict(prune_model, testing_set, type="class")
mean(tree_pred1 != High[test])Надо сказать, в данном конкретном случае отсечение не очень-то и помогло: при данных значениях seed получится 24% вместо 24.8%. В других случаях с помощью этого метода иногда получается добиться лучших результатов (хотя как мы увидим дальше, сейчас тоже получилось неплохо).
Пользуясь случаем, расскажу немного о том, что такое «хорошо» и «плохо». На этом этапе я хочу вернуть читателя в реальный мир и показать, насколько все на самом деле может быть плохо. Если поменять значение seed, можно получить, например, 30% - да так, что никакое отсечение не поможет. Все дело в данных: здесь мы делаем случайную выборку из не самых лучших данных, и поэтому в зависимости от начального значения генератора результат может очень сильно меняться. В задачах анализа данных это происходит довольно часто. Данные редко бывают настолько хороши, чтобы работа с ними была сразу приятна, а результаты стабильны и поражали нас значениями точности и полноты.
Кстати, чуть не забыл! Надо бы посчитать соответствующие величины для полученных нами только что результатов. Для начала сделаем это для нашей оригинальной модели:
t = table(pred=tree_pred, true=High[test])Если вывести ее на консоль, мы увидим:
true
pred No Yes
No 66 23
Yes 10 34Эта таблица как раз и представляет собой вычисленные значения TP, FP, TN, FN. Теперь легко написать функцию, которая сможет рассчитывать точность и полноту:
check <- function(res) {
tn = res[1,1]
tp = res[2,2]
fp = res[1,2]
fn = res[2,1]
prec <- tp / (tp + fp)
recall <- tp / (tp + fn)
f1 <- 2 * tp / (2 * tp + fp + fn)
list(precision=prec, recall=recall, f1=f1)
}Итак, для оригинальной модели соответствующие значения будут:
$precision
[1] 0.5964912
$recall
[1] 0.7727273
$f1
[1] 0.6732673Теперь все то же самое, только уже для модели с отсечением:
t1 = table(pred=tree_pred1, true=High[test])
check(t1)Несмотря на то, что при использовании mean разница между моделями не казалось уж такой существенной, точность модели возросла более чем на 5%, а F-мера - на 2%, хотя полнота упала на 2%:
$precision
[1] 0.6491228
$recall
[1] 0.755102
$f1
[1] 0.6981132Итак, когда мы немного разобрались с тем, как решать задачу классификации с помощью деревьев решений, настало время рассказать о том, какие еще пакеты доступны для работы с ними. Тем более, что методы визуализации для пакета tree, как мы видели выше, не так хороши.
Визуализация деревьев
Для начала следует упомянуть пакет party, который имеет довольно приличную систему визуализации (см. рис 4):
library(party)
ct = ctree(High~., training_set)
plot(ct)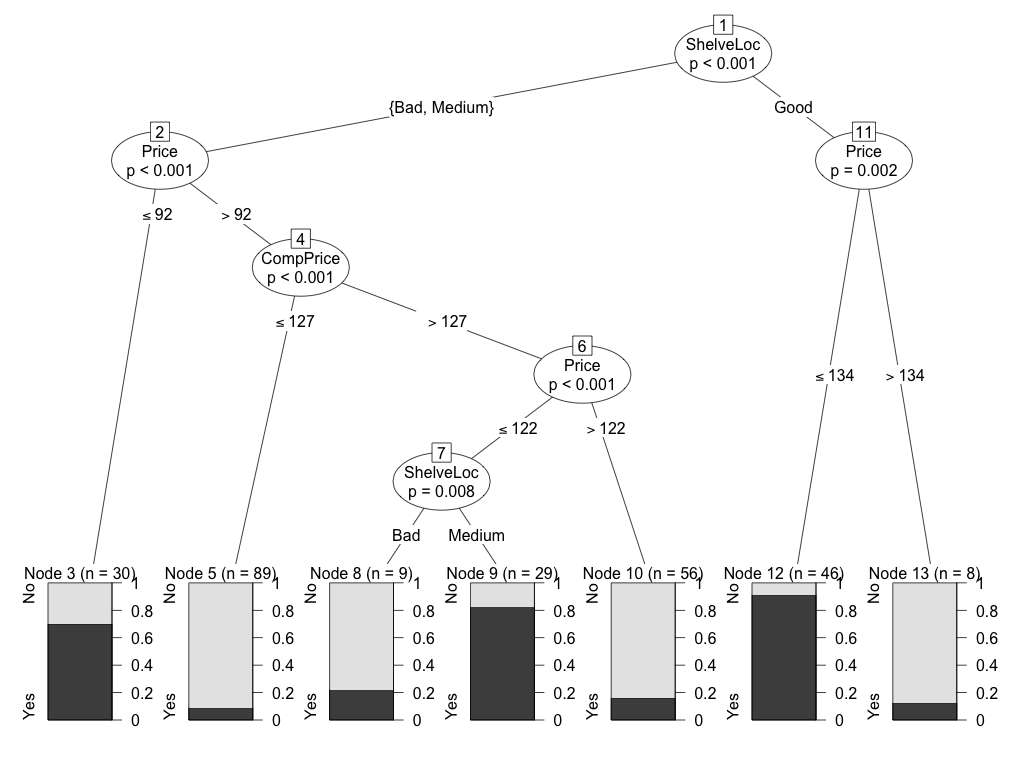
Еще один приятный в использовании вариант - это пакет rpart и пакет для визуализации rpart.plot:
library(rpart)
library(rpart.plot)
rp = rpart(High~., training_set)
prp(rp)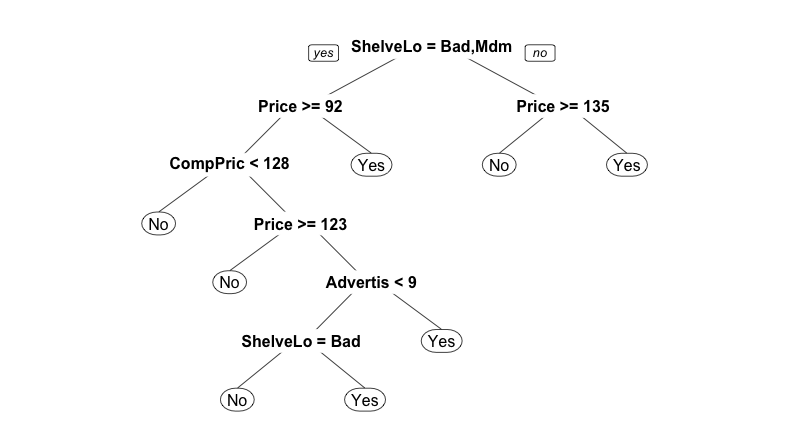
Если воспользоваться функций fancyRpartPlot из пакета rattle, то можно получить прекрасное изображение, как показано на рис 6.
library(rattle)
fancyRpartPlot(rp)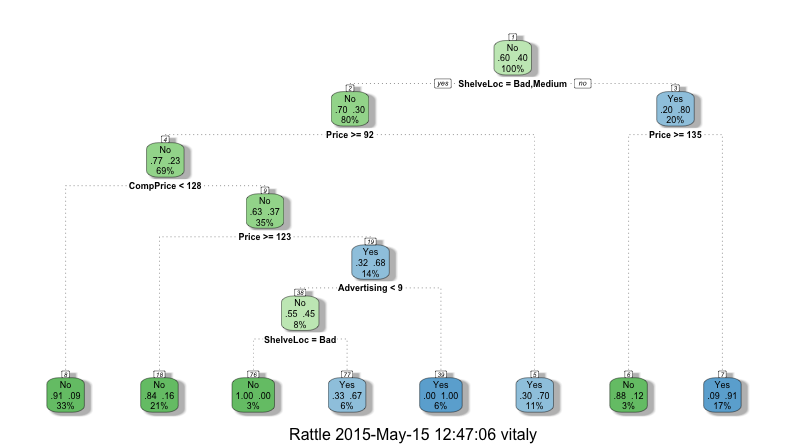
Вместо заключения
В следующих статьях я расскажу, про работу с другими алгоритмами классификации (такими как наивный байессовский классификатор и метод опорных векторов), а также с нейронными сетями и алгоритмом Random Forest. Более того, я немного расскажу про то, как это работает на самом деле.