Содержание статьи
- Немного теории
- Базовые функции стандарта
- Сложение двух двоичных векторов по модулю 2
- Побитовое исключающее ИЛИ над 512-битными блоками
- Нелинейное биективное преобразование (преобразование S)
- Перестановка байтов (преобразование P)
- Линейное преобразование (преобразование L)
- Пишем все остальное
- Первый этап (инициализация)
- Второй этап
- Третий этап
- Функция GOSTHashUpdate
- Функция GOSTHashFinal
- Считаем хеш-сумму файла
- Заключение
Стандарт ГОСТ 34.11—2012 пришел на смену ГОСТ 34.11—94, который к настоящему времени уже считается потенциально уязвимым (хотя до 2018 года ГОСТ 1994 года выпуска все же применять не возбраняется). Отечественные стандарты хеширования обязательны к применению в продуктах, которые будут крутиться в ответственных и критических сферах и для которых обязательно прохождение сертификации в уполномоченных органах (ФСТЭК, ФСБ и подобных). ГОСТ 34.11—2012 был разработан Центром защиты информации и специальной связи ФСБ России с участием открытого акционерного общества «Информационные технологии и коммуникационные системы» (ИнфоТеКС). В основу стандарта 2012 года была положена функция хеширования под названием «Стрибог» (если что, такое имя носил бог ветра в древнеславянской мифологии).


Xakep #210. Краткий экскурс в Ethereum
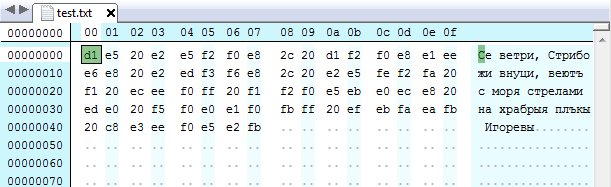
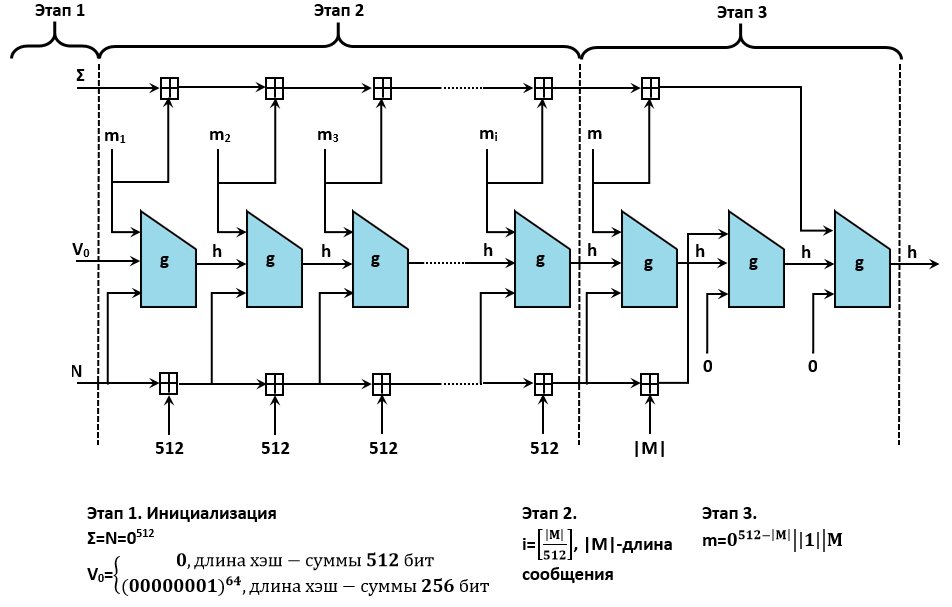
Хеш-функция «Стрибог» может иметь две реализации с результирующим значением длиной 256 или 512 бит. На вход функции подается сообщение, для которого необходимо вычислить хеш-сумму. Если длина сообщения больше 512 бит (или 64 байт), то оно делится на блоки по 512 бит, а оставшийся кусочек дополняется нулями с одной единичкой до 512 бит (или до 64 байт). Если длина сообщения меньше 512 бит, то оно сразу дополняется нулями с единичкой до полных 512 бит.
Немного теории
Основу хеш-функции «Стрибог» составляет функция сжатия (g-функция), построенная на блочном шифре, построенном с помощью конструкции Миягучи — Пренеля, признанной одной из наиболее стойких.

В целом хеширование производится в три этапа. Первый этап — инициализация всех нужных параметров, второй этап представляет собой так называемую итерационную конструкцию Меркла — Дамгорда с процедурой МД-усиления, третий этап — завершающее преобразование: функция сжатия применяется к сумме всех блоков сообщения и дополнительно хешируется длина сообщения и его контрольная сумма.
WARNING
При чтении ГОСТа учти, что во всех 64-байтовых массивах (в том числе и в массивах значений итерационных констант C1 — C12) нулевой байт находится в конце массива, а шестьдесят третий, соответственно, в начале.
Итак, после краткого и небольшого погружения в теорию начинаем кодить...
Базовые функции стандарта
Поскольку при вычислении хеша мы имеем дело с 64-байтовыми блоками (в стандарте они представлены 512-разрядными двоичными векторами), для начала определим этот самый двоичный вектор:
#define BLOCK_SIZE 64 // Размер блока — 64 байта
...
typedef uint8_t vect[BLOCK_SIZE]; // Определяем тип vect как 64-байтовый массивСложение двух двоичных векторов по модулю 2
Здесь все предельно просто. Каждый байт первого вектора ксорится с соответствующим байтом второго вектора, и результат пишется в третий (выходной) вектор:
static void GOSTHashX(const uint8_t *a, const uint8_t *b, uint8_t *c)
{
int i;
for (i = 0; i < 64; i++)
c[i] = a[i]^b[i];
}Побитовое исключающее ИЛИ над 512-битными блоками
В тексте ГОСТа название данной операции звучит как сложение в кольце вычетов по модулю 2 в степени n. Такая фраза кого угодно может вогнать в уныние, но на самом деле ничего сложного и страшного в ней нет. Два исходных 64-байтовых вектора представляются как два больших числа, далее они складываются, и переполнение, если оно появляется, отбрасывается:
static void GOSTHashAdd512(const uint8_t *a, const uint8_t *b, uint8_t *c)
{
int i;
int internal = 0;
for (i = 0; i < 64; i++)
{
internal = a[i] + b[i] + (internal >> 8);
c[i] = internal & 0xff;
}
}Нелинейное биективное преобразование (преобразование S)
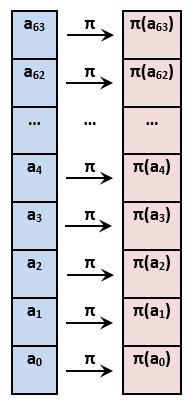
При биективном отображении каждому элементу одного множества соответствует ровно один элемент другого множества (более подробно про биекцию можешь почитать в Википедии). То есть это просто банальная подстановка байтов в исходном векторе по определенному правилу. В данном случае правило задается массивом из 256 значений:
static const unsigned char Pi[256] = {
252, 238, 221, ... 99, 182
};Здесь для экономии места показаны не все значения, определенные в стандарте, а только три первых и два последних. Когда будешь писать код, не забудь про остальные.
Итак, если в исходном векторе у нас встречается какой-либо байт со значением, например, 23 (в десятичном выражении), то вместо него мы пишем байт из массива Pi, имеющий порядковый номер 23, и так далее. В общем, код функции преобразования S получается такой:
static void GOSTHashS(uint8_t *state)
{
int i;
vect internal;
for (i = 63; i >= 0; i--)
internal[i] = Pi[state[i]];
memcpy(state, internal, BLOCK_SIZE);
}
Перестановка байтов (преобразование P)
Преобразование P — простая перестановка байтов в исходном массиве в соответствии с правилом, определяемым массивом Tau размером в 64 байта:
static const unsigned char Tau[64] = {
0, 8, 16, 24, 32, ... 55, 63
};Здесь, так же как и в предыдущем случае, для экономии места показаны не все значения массива Tau.
Перестановка выполняется следующим образом: сначала идет нулевой элемент исходного вектора, далее — восьмой, потом — шестнадцатый и так далее до последнего элемента. Код функции напишем так:
static void GOSTHashP(uint8_t *state)
{
int i;
vect internal;
for (i = 63; i >= 0; i--)
internal[i] = state[Tau[i]];
memcpy(state, internal, BLOCK_SIZE);
}Линейное преобразование (преобразование L)
Это преобразование носит название «умножение справа на матрицу A над полем Галуа GF(2)» и по сравнению с первыми двумя будет немного посложнее (по крайней мере, вкурить всю суть от и до с первого прочтения стандарта удается далеко не всем). Итак, есть матрица линейного преобразования A, состоящая из 64 восьмибайтовых чисел (здесь приведена не в полном объеме):
static const unsigned long long A[64] = {
0x8e20faa72ba0b470,
0x47107ddd9b505a38,
0xad08b0e0c3282d1c,
0xd8045870ef14980e,
0x6c022c38f90a4c07,
...
...
0xc83862965601dd1b,
0x641c314b2b8ee083
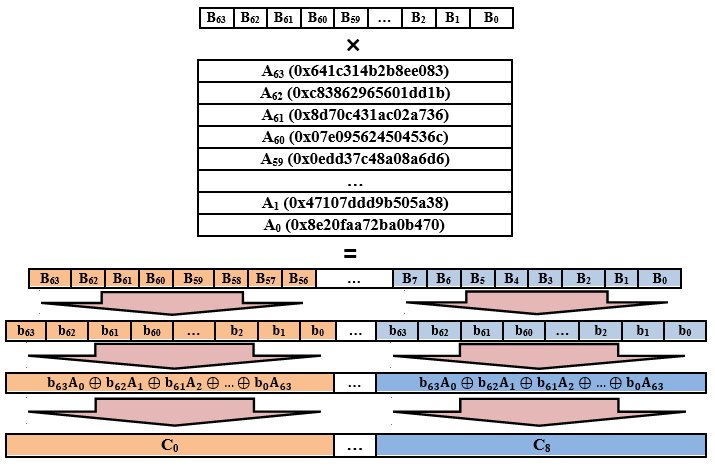
};Исходный вектор делится на порции размером по 8 байт, каждая из этих порций интерпретируется в виде 64-разрядного двоичного представления. Далее берется очередная порция, каждому биту из этой порции ставится в соответствие строка из матрицы A. Если очередной бит равен нулю, то соответствующая ему строка из матрицы A вычеркивается; если очередной бит равен единице, то соответствующая ему строка из матрицы A остается. После всего этого оставшиеся строки из матрицы линейного преобразования ксорятся, и получившееся число записывается в виде очередной восьмибайтовой порции в результирующий вектор. Код выглядит следующим образом:
static void GOSTHashL(uint8_t *state)
{
// Делим исходный вектор на восьмибайтовые порции
uint64_t* internal_in = (uint64_t*)state;
uint64_t internal_out[8];
memset(internal_out, 0x00, BLOCK_SIZE);
int i, j;
for (i = 7; i >= 0; i--)
{
// Если очередной бит равен 1, то ксорим очередное
// значение матрицы A с предыдущими
for (j = 63; j >= 0; j--)
if ((internal_in[i] >> j) & 1)
internal_out[i] ^= A[63 - j];
}
memcpy(state, internal_out, 64);
}
Пишем все остальное
Имея в наличии все необходимые базовые преобразования, определенные стандартом, можно приступить непосредственно к реализации алгоритма «Стрибог» в целом.
Для начала определим структуру, в которую будем складывать все исходные, промежуточные и конечные результаты вычислений:
typedef struct GOSTHashContext
{
vect buffer; // Буфер для очередного блока хешируемого сообщения
vect hash; // Итоговый результат вычислений
vect h; // Промежуточный результат вычислений
vect N; //
vect Sigma; / /Контрольная сумма
vect v_0; // Инициализационный вектор
vect v_512; // Инициализационный вектор
size_t buf_size; // Размер оставшейся части сообщения
// (которая оказалась меньше очередных 64 байт)
int hash_size; // Размер хеш-суммы (512 или 256 бит)
} TGOSTHashContext;Далее напишем преобразование E, которое является частью функции сжатия. В этом преобразовании задействовано двенадцать так называемых итерационных констант (C1 — C12), на основе которых вычисляются раундовые ключи K. Для вычисления этих раундовых ключей определим функцию GOSTHashGetKey, которая представляет собой сочетание преобразований S, P и L, а также побайтного сложения по модулю 2:
static void GOSTHashGetKey(uint8_t *K, int i)
{
GOSTHashX(K, C[i], K);
GOSTHashS(K);
GOSTHashP(K);
GOSTHashL(K);
}Для этой функции необходимо описать итерационные константы, которых, как мы уже говорили, двенадцать штук (для краткости здесь эти константы показаны не в полном объеме):
static const unsigned char C[12] [64] = {
{0x07, 0x45, 0xa6, ... , 0xb1},
{0xb7, 0x9b, 0xb1, ... , 0x6f},
{0xb2, 0x0a, 0xba, ... , 0xf5},
{0x2e, 0xd1, 0xe3, ... , 0xef},
{0x57, 0xfe, 0x6c, ... , 0x4b},
{0x6e, 0x7d, 0x64, ... , 0xae},
{0x93, 0xd4, 0x14, ... , 0xf4},
{0x1e, 0xe7, 0x02, ... , 0x9b},
{0xdb, 0x5a, 0x23, ... , 0x37},
{0xed, 0x9c, 0x45, ... , 0xab},
{0x1b, 0x2d, 0xf3, ... , 0x7b},
{0x20, 0xd7, 0x1b, ... , 0x37}
};Если ты попытаешься сравнить приведенные выше константы с текстом стандарта, то увидишь, что эти самые константы записаны «задом наперед». Дело в том, что все байтовые массивы (в том числе и строки тестовых примеров) в тексте стандарта описаны таким образом, что нулевой их элемент находится в конце массива, а не в начале, как мы привыкли, поэтому строки перед использованием надо «переворачивать».
Далее пишем саму функцию преобразования E:
static void GOSTHashE(uint8_t *K, const uint8_t *m, uint8_t *state)
{
int i;
memcpy(K, K, BLOCK_SIZE);
GOSTHashX(m, K, state);
for(i = 0; i < 12; i++)
{
GOSTHashS(state);
GOSTHashP(state);
GOSTHashL(state);
GOSTHashGetKey(K, i);
GOSTHashX(state, K, state);
}
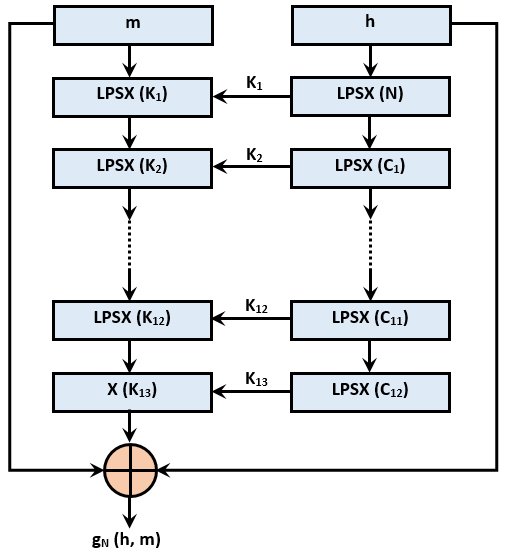
}И, используя эти функции, пишем самую главную функцию алгоритма «Стрибог» — функцию сжатия g:
static void GOSTHashG( uint8_t *h, uint8_t *N, const uint8_t *m)
{
vect K, internal;
GOSTHashX(N, h, K);
GOSTHashS(K);
GOSTHashP(K);
GOSTHashL(K);
GOSTHashE(K, m, internal);
GOSTHashX(internal, h, internal);
GOSTHashX(internal, m, h);
}
В самом начале мы говорили, что хеширование выполняется блоками по 64 байта, а последний блок, если он меньше 64 байт, дополняется нулями с одной единичкой. Для этой операции вполне подойдет функция GOSTHashPadding:
static void GOSTHashPadding(TGOSTHashContext *CTX)
{
vect internal; // Промежуточный вектор
if (CTX->buf_size < BLOCK_SIZE)
{
memset(internal, 0x00, BLOCK_SIZE); // Обнуляем промежуточный вектор
memcpy(internal, CTX->buffer, CTX->buf_size); // Пишем остаток сообщения
// в промежуточный вектор
internal[CTX->buf_size] = 0x01; // Добавляем в нужное место единичку
memcpy(CTX->buffer, internal, BLOCK_SIZE); // Кладем все, что получилось, обратно
}
}Теперь открываем руководящий документ на шестой странице и внимательно разбираемся с этапами вычисления столь нужной нам хеш-функции.
Первый этап (инициализация)
Как ясно из названия, этот этап необходим для первоначального задания значений всех переменных:
void GOSTHashInit(TGOSTHashContext *CTX, uint16_t hash_size)
{
memset(CTX, 0x00, sizeof(TGOSTHashContext)); // Обнуляем все переменные
// базовой структуры
if (hash_size == 256)
memset(CTX->h, 0x01, BLOCK_SIZE); // Длина хеша 256 бит
else
memset(CTX->h, 0x00, BLOCK_SIZE); // Длина хеша 512 бит
CTX->hash_size = hash_size;
CTX->v_512[1] = 0x02; // Инициализируем вектор v_512
}Второй этап
На этом этапе мы хешируем отдельные блоки размером в 512 бит (или 64 байта) до тех пор, пока они не кончатся. Этап состоит из функции сжатия и двух операций исключающего ИЛИ (с их помощью формируется контрольная сумма):
static void GOSTHashStage_2(TGOSTHashContext *CTX, const uint8_t *data)
{
GOSTHashG(CTX->h, CTX->N, data);
GOSTHashAdd512(CTX->N, CTX->v_512, CTX->N);
GOSTHashAdd512(CTX->Sigma, data, CTX->Sigma);
}Третий этап
На третьем этапе мы хешируем остаток, который не попал в очередной 64-байтный блок из-за того, что его размер меньше. Далее формируем контрольную сумму всего сообщения с учетом его длины и вычисляем окончательный результат. Выглядит это все так:
static void GOSTHashStage_3(TGOSTHashContext *CTX)
{
vect internal;
memset(internal, 0x00, BLOCK_SIZE);
// Формируем строку с размером сообщения
internal[1] = ((CTX->buf_size * 8) >> 8) & 0xff;
internal[0] = (CTX->buf_size * 8) & 0xff;
GOSTHashPadding(CTX); // Дополняем оставшуюся часть до полных
// 64 байт
GOSTHashG(CTX->h, CTX->N, (const uint8_t*)&(CTX->buffer));
// Формируем контрольную сумму сообщения
GOSTHashAdd512(CTX->N, internal, CTX->N);
GOSTHashAdd512(CTX->Sigma, CTX->buffer, CTX->Sigma);
GOSTHashG(CTX->h, CTX->v_0, (const uint8_t*)&(CTX->N));
GOSTHashG(CTX->h, CTX->v_0, (const uint8_t*)&(CTX->Sigma));
memcpy(CTX->hash, CTX->h, BLOCK_SIZE); // Записываем результат
// в нужное место
}Разобравшись со всеми этапами, сложим все в единое целое. Весь процесс будет описан в трех функциях:
GOSTHashInit(она у нас уже есть);GOSTHashUpdate(туда мы поместим все итерации второго этапа);GOSTHashFinal(там мы завершим весь процесс третьим этапом).
Функция GOSTHashUpdate
Объявим эту функцию таким образом:
void GOSTHashUpdate(TGOSTHashContext *CTX,
const uint8_t *data,
size_t len)Как уже неоднократно говорилось, хеширование производится блоками по 64 байта, поэтому в начале функции напишем следующее:
while((len > 63) && (CTX->buf_size) == 0)
{
GOSTHashStage_2(CTX, data);
data += 64;
len -= 64;
}Поскольку при чтении файла мы его будем читать по кусочкам, длина которых задается при использовании функции fread, то при слишком длинном файле мы можем потерять остаток файла и, соответственно, неправильно посчитать хеш-сумму. Чтобы этого избежать, необходимо в нашу функцию GOSTHashUpdate добавить следующий код:
size_t chk_size; // Объем незаполненной части буфера
while (len)
{
chk_size = 64 - CTX->buf_size;
if (chk_size > len)
chk_size = len;
// Дописываем незаполненную часть буфера
memcpy(&CTX->buffer[CTX->buf_size], data, chk_size);
CTX->buf_size += chk_size;
len -= chk_size;
data += chk_size;
if (CTX->buf_size == 64)
{
// Если буфер заполнился полностью, то
// делаем еще один второй этап
GOSTHashStage_2(CTX, CTX->buffer);
CTX->buf_size = 0;
}
}Функция GOSTHashFinal
Здесь все просто:
void GOSTHashFinal(TGOSTHashContext *CTX)
{
// Запускаем третий этап
GOSTHashStage_3(CTX);
CTX->buf_size = 0;
}Считаем хеш-сумму файла
Вот мы и подошли к завершающему этапу написания кода, позволяющего посчитать хеш-сумму по алгоритму «Стрибог». Осталось считать нужный файл в заранее отведенный участок памяти и поочередно вызвать функции GOSTHashUpdate и GOSTHashFinal:
FILE_BUFFER_SIZE = 4096 // Определяем объем буфера для считывания файла
...
buffer = malloc((size_t) FILE_BUFFER_SIZE); // Отводим участок памяти
// для буфера, куда будем
// читать файл
...
// Поэтапно читаем файл
while ((len = fread(buffer, (size_t) 1, (size_t) FILE_BUFFER_SIZE, file)))
// Запускаем второй этап, пока не прочтем весь файл
GOSTHashUpdate(CTX, buffer, len);
// Запускаем третий этап
GOSTHashFinal(CTX);
// В CTX->hash получаем нужный нам результат
...После завершения в зависимости от нужной нам длины хеш-суммы берем значение CTX->hash полностью (длина хеша 512 бит) либо берем от CTX->hash последние 32 байта.
Не забудь про исходники
Весь код: классическую реализацию алгоритма (в полном соответствии с ГОСТом), усовершенствованную реализацию (с предварительным расчетом значений преобразований S и L), а также код предварительного расчета значений преобразований S и L — ты найдешь в приложении к этому номеру.
Заключение
Наверняка у тебя промелькнула мысль о ресурсоемкости данного алгоритма и возможных способах увеличения быстродействия. Очевидные приемы типа применения выравнивания при описании всех используемых структур, переменных и участков памяти, скорее всего, ощутимого эффекта не дадут, но в этом алгоритме есть возможность заранее посчитать некоторые значения и использовать при написании кода в дальнейшем именно их.
Если внимательно почитать стандарт (особенно страницы 3 и 4), то выяснится, что преобразования S и L можно выполнить заранее и сформировать восемь массивов по 256 восьмибайтовых чисел, в которых будут содержаться все возможные значения этих двух преобразований. Помимо этого, при вычислении хеш-суммы с использованием заранее рассчитанных значений можно сразу сделать и нужные перестановки в соответствии с преобразованием P. В общем, весь нужный код (вычисление хеша классическим алгоритмом, предварительный расчет значений преобразований S и L и вычисление хеша с помощью заранее просчитанных значений) найдешь в приложении к этой статье. Бери, разбирайся, пользуйся...
WWW
Сам текст ГОСТ 34.11—2012 можно скачать здесь
Реализация ГОСТ 34.11—2012 на Go
Реализация ГОСТ 34.11—2012 на Python
Весьма примечательная статья про стойкость алгоритма «Стрибог» к некоторым видам атак