Содержание статьи
Этот алгоритм представляет собой точную копию алгоритма блочного шифрования из старого ГОСТ 28147—89, за одним исключением. В новом ГОСТ 34.12—2015 определена и задана таблица перестановок для нелинейного биективного преобразования, которая в старом ГОСТ 28147—89 отсутствовала, и задание ее элементов полностью отдавалось в руки людей, реализующих данный алгоритм. Теоретически, если определить элементы таблицы перестановок самостоятельно и сохранить таблицу в тайне, это позволит повысить стойкость алгоритма шифрования (за счет этого фактически увеличивается длина ключа), однако, как видим, разработчики ГОСТ 34.12—2015 решили лишить самостоятельности пользователей стандарта.
Как уже было сказано, длина шифруемого блока в алгоритме «Магма» — 64 бита. Длина ключа шифрования — 256 бит.
WARNING
При чтении ГОСТа учти, что во всех 8-байтовых массивах тестовых последовательностей нулевой байт находится в конце массива, а седьмой, соответственно, в начале (если ты внимательно читал статьи про «Стрибог» и «Кузнечик», то эта особенность наших криптостандартов тебе должна быть знакома).
Немного теории
В описываемом алгоритме блок, подлежащий зашифровыванию (напомню, его длина 64 бита), разделяется на две равные по длине (32 бита) части — правую и левую. Далее выполняется тридцать две итерации с использованием итерационных ключей, получаемых из исходного 256-битного ключа шифрования.

Во время каждой итерации (за исключением тридцать второй) с правой и левой половиной зашифровываемого блока производится одно преобразование, основанное на сети Фейстеля. Сначала правая часть складывается по модулю 32 с текущим итерационным ключом, затем полученное 32-битное число делится на восемь 4-битных и каждое из них с использованием таблицы перестановки преобразуется в другое 4-битное число (если помнишь, то в предыдущих двух статьях это называлось нелинейным биективным преобразованием). После этого преобразования полученное число циклически сдвигается влево на одиннадцать разрядов. Далее результат ксорится с левой половиной блока. Получившееся 32-битное число записывается в правую половину блока, а старое содержимое правой половины переносится в левую половину блока.
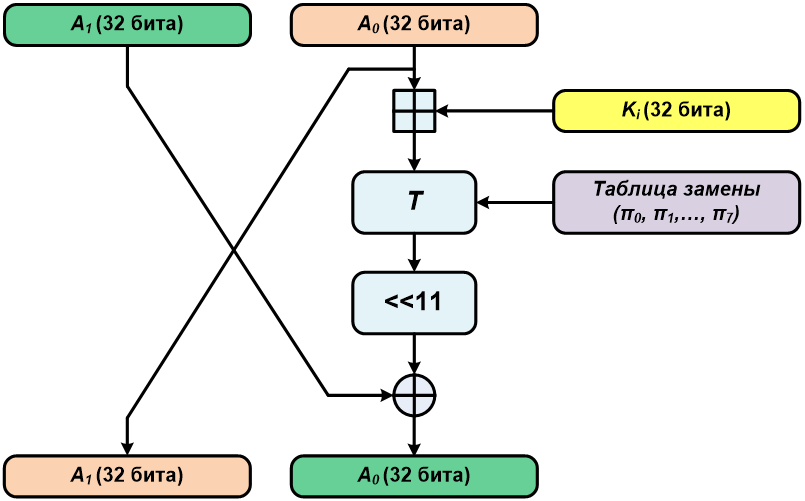
В ходе последней (тридцать второй) итерации так же, как описано выше, преобразуется правая половина, после чего полученный результат пишется в левую часть исходного блока, а правая половина сохраняет свое значение.
Итерационные ключи получаются из исходного 256-битного ключа. Исходный ключ делится на восемь 32-битных подключей, и далее они используются в следующем порядке: три раза с первого по восьмой и один раз с восьмого по первый.
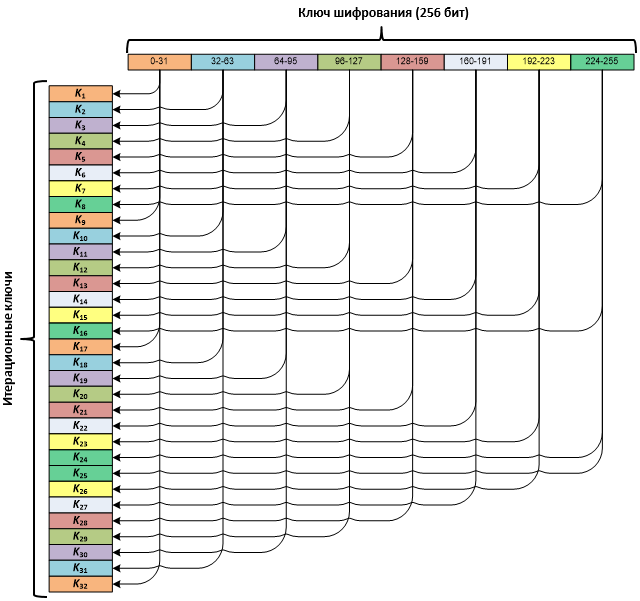
Для расшифровывания используется такая же последовательность итераций, как и при зашифровывании, но порядок следования ключей изменяется на обратный.

Итак, после краткого и небольшого погружения в теорию начинаем кодить...
Базовые функции стандарта
Поскольку в алгоритме используются 32-битные блоки (в виде так называемых двоичных векторов), для начала определим этот самый блок:
// Размер блока 4 байта (или 32 бита)
#define BLOCK_SIZE 4
...
// Определяем тип vect как 4-байтовый массив
typedef uint8_t vect[BLOCK_SIZE];
Сложение двух двоичных векторов по модулю 2
Каждый байт первого вектора ксорится с соответствующим байтом второго вектора, и результат пишется в третий (выходной) вектор:
static void GOST_Magma_Add(const uint8_t *a, const uint8_t *b, uint8_t *c)
{
int i;
for (i = 0; i < BLOCK_SIZE; i++)
c[i] = a[i]^b[i];
}
Сложение двух двоичных векторов по модулю 32
Данная функция аналогична функции под названием «сложение в кольце вычетов по модулю 2 в степени n» из алгоритма «Стрибог», за исключением того, что n в нашем случае будет равно 32, а не 512, как в стандарте «Стрибог». Два исходных 4-байтовых вектора представляются как два 32-битных числа, далее они складываются, переполнение, если оно появляется, отбрасывается:
static void GOST_Magma_Add_32(const uint8_t *a, const uint8_t *b, uint8_t *c)
{
int i;
unsigned int internal = 0;
for (i = 3; i >= 0; i--)
{
internal = a[i] + b[i] + (internal >> 8);
c[i] = internal & 0xff;
}
}
Нелинейное биективное преобразование (преобразование T)
В отличие от алгоритмов «Стрибог» и «Кузнечик» (кстати, там это преобразование называется S-преобразованием) таблица перестановок здесь используется другая:
static unsigned char Pi[8][16]=
{
{1,7,14,13,0,5,8,3,4,15,10,6,9,12,11,2},
{8,14,2,5,6,9,1,12,15,4,11,0,13,10,3,7},
{5,13,15,6,9,2,12,10,11,7,8,1,4,3,14,0},
{7,15,5,10,8,1,6,13,0,9,3,14,11,4,2,12},
{12,8,2,1,13,4,15,6,7,0,10,5,3,14,9,11},
{11,3,5,8,2,15,10,13,14,1,7,4,12,9,6,0},
{6,8,2,3,9,10,5,12,1,14,4,7,11,13,0,15},
{12,4,6,2,10,5,11,9,14,8,13,7,0,3,15,1}
};
Поскольку в тексте стандарта (по неведомой традиции) нулевой байт пишется в конце, а последний в начале, то для корректной работы программы строки таблицы необходимо записывать в обратном порядке, а не так, как изложено в стандарте.
Код самой функции преобразования T получается такой:
static void GOST_Magma_T(const uint8_t *in_data, uint8_t *out_data)
{
uint8_t first_part_byte, sec_part_byte;
int i;
for (i = 0; i < 4; i++)
{
// Извлекаем первую 4-битную часть байта
first_part_byte = (in_data[i] & 0xf0) >> 4;
// Извлекаем вторую 4-битную часть байта
sec_part_byte = (in_data[i] & 0x0f);
// Выполняем замену в соответствии с таблицей подстановок
first_part_byte = Pi[i * 2][first_part_byte];
sec_part_byte = Pi[i * 2 + 1][sec_part_byte];
// «Склеиваем» обе 4-битные части обратно в байт
out_data[i] = (first_part_byte << 4) | sec_part_byte;
}
}
Продолжение доступно только участникам
Вариант 1. Присоединись к сообществу «Xakep.ru», чтобы читать все материалы на сайте
Членство в сообществе в течение указанного срока откроет тебе доступ ко ВСЕМ материалам «Хакера», позволит скачивать выпуски в PDF, отключит рекламу на сайте и увеличит личную накопительную скидку! Подробнее
Вариант 2. Открой один материал
Заинтересовала статья, но нет возможности стать членом клуба «Xakep.ru»? Тогда этот вариант для тебя! Обрати внимание: этот способ подходит только для статей, опубликованных более двух месяцев назад.
Я уже участник «Xakep.ru»















